что такое колебательный контур

Содержание

Резонанс токов

Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:

Чему будет равняться резонансный ток I_рез? Считаем по закону Ома:

I_рез = U_ген/R_рез, где R_рез= L/CR.

Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток I_кон, который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.

Что такое ёмкость конденсатора?

Ёмкость конденсатора представляет собой отношение заряда конденсатора к напряжению, под которым он находится. Посчитать эту величину можно очень просто с помощью математической формулы:

C = (e0*S)/d, гдеe0 — диэлектрическая проницаемость материала диэлектрика (табличная величина), S — площадь обкладок конденсатора, d — расстояние между пластинами.

Зависимость ёмкости конденсатора от расстояния между обкладками объясняется явлением электростатической индукции: чем меньше расстояние между пластинами, тем сильнее они влияют друг на друга (по закону Кулона), тем больше заряд обкладок и меньше напряжение. А при уменьшении напряжения увеличивается значение ёмкости, так как её также можно описать следующей формулой:

C = q/U, гдеq — заряд в кулонах.

Стоит поговорить о единицах измерения этой величины. Ёмкость измеряется в фарадах. 1 фарад — достаточно большая величина, поэтому существующие конденсаторы (но не ионисторы) имеют ёмкость, измеряемую в пикофарадах (одна триллионная фарада).

Катушка индуктивности

Давайте подробнее рассмотрим все тонкости работы катушки индуктивности и лучше поймём её функцию в колебательном контуре. Как мы уже говорили, сопротивление этого элемента стремится к нулю. Таким образом, при подключении к цепи постоянного тока произошло бы короткое замыкание. Однако если подключать катушку в цепь переменного тока, она работает исправно. Это позволяет сделать вывод о том, что элемент оказывает сопротивление переменному току.

Но почему это происходит и как возникает сопротивление при переменном токе? Для ответа на этот вопрос нам нужно обратиться к такому явлению, как самоиндукция. При прохождении тока по катушке в ней возникает электродвижущая сила (ЭДС), которая создаёт препятствие изменению тока. Величина этой силы зависит от двух факторов: индуктивности катушки и производной силы тока по времени. Математически эта зависимость выражается через уравнение:

E = -L*I'(t) , где E — значение ЭДС, L — величина индуктивности катушки (для каждой катушки она разная и зависит от количества мотков обмотки и их толщины), I'(t) — производная силы тока по времени (скорость изменения силы тока).

Сила постоянного тока со временем не изменяется, поэтому сопротивления при его воздействии не возникает.

Но при переменном токе все его параметры постоянно изменяются по синусоидальному или косинусоидальному закону, вследствие чего возникает ЭДС, препятствующая этим изменениям. Такое сопротивление называют индукционным и вычисляют по формуле:

XL = w*L, где w — частота колебаний контура, L — индуктивность катушки.

Сила тока в соленоиде линейно нарастает и убывает по различным законам. Это значит, что если прекратить подачу тока в катушку, она будет продолжать некоторое время отдавать заряд в цепь. А если при этом резко прервать подачу тока, то будет происходить удар из-за того, что заряд будет пытаться распределиться и выйти из катушки. Это — серьёзная проблема в промышленном производстве. Такой эффект (хотя и не совсем связанный с колебательным контуром) можно наблюдать, например, при вытаскивании вилки из розетки. При этом проскакивает искра, которая в таких масштабах не в силах нанести вред человеку. Она обусловлена тем, что магнитное поле не исчезает сразу, а постепенно рассеивается, индуцируя токи в других проводниках. В промышленных масштабах сила тока во много раз больше привычных нам 220 вольт, поэтому при прерывании цепи на производстве могут возникнуть искры такой силы, что причинят немало вреда как заводу, так и человеку.

Катушка — это основа того, из чего колебательный контур состоит. Индуктивности последовательно включённых соленоидов складываются. Далее мы подробнее рассмотрим все тонкости строения этого элемента.

Где применяется колебательный контур?

Самое знакомое нам применение составляющих контура — это электромагниты. Они, в свою очередь, используются в домофонах, электродвигателях, датчиках и во многих других не столь обыденных областях. Другое применение — генератор колебаний. На самом деле это использование контура нам очень знакомо: в этом виде он применяется в микроволновке для создания волн и в мобильной и радиосвязи для передачи информации на расстояние. Всё это происходит благодаря тому, что колебания электромагнитных волн можно закодировать таким образом, что станет возможным передавать информацию на большие расстояния.

Катушка индуктивности сама по себе может использоваться как элемент трасформатора: две катушки с разным числом обмоток могут передавать с помощью электромагнитного поля свой заряд. Но так как характеристики соленоидов различаются, то и показатели тока в двух цепях, к которым подключены эти две индуктивности, будут различаться. Таким образом можно преобразовывать ток с напряжением в 220 вольт в ток с напряжением в 12 вольт.

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:

Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L, а на конденсаторе U_C = IX_C. А так как при резонансе у нас X_L= X_C, то получаем что U_L= U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Принцип работы параллельного колебательного контура

Давайте подцепим к генератору частоты реальный параллельный колебательный контур

Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.

Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.

Реактивное сопротивление катушки выражается по формуле

а конденсатора по формуле

Более подробно про это можно прочитать в этой статье.

Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки XL и конденсатора XC уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.

RLC-контур

Кроме как в механических системах, к примеру, в таких, маятник или же грузило на пружине, свободные колебания могут возникать также и в электрических цепях, самым простым примером чего может послужить последовательный RLC-контур, изображенный на рис. 2.2.1.

Рисунок 2.2.1.Последовательный RLC-контур.

Находясь в положении 1, ключ К позволяет источнику зарядить конденсатор до некоего напряжения δ. Процесс разрядки ранее заряженного конденсатора провоцируется переключением ключа К во второе положение и происходит через катушку индуктивности L и резистор R. При выполнении определенных условий данный процесс может приобретать характер колебательного.

Для не содержащей внешнего источника тока замкнутой RLC-цепи закон Ома представляет из себя выражение:

JR+U=-LdJdt.

В данной формуле U=qC – напряжение на конденсаторе, q является обозначением заряда конденсатора, а J=dqdt – ток в цепи. Правой частью соотношения является выражение ЭДС самоиндукции катушки. В случае, когда заряд конденсатора q (t) берется как переменная величина, описывающее свободные колебания в RLC-контуре уравнение может быть приведено к виду:

q··+RLq·+1LCq=.

Для начала рассмотрим такую ситуацию, в которой электромагнитные потери энергии в контуре равны нулю. В таком случае:

q··+ω2q=.

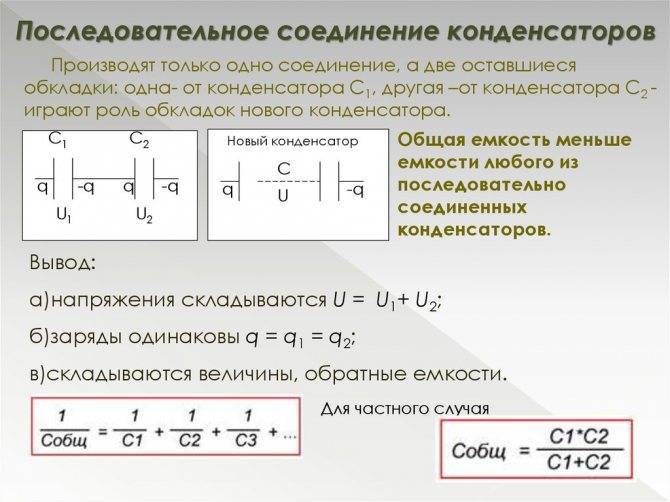
Примем обозначение ω2=1LC. Данным чуть выше уравнением описывается процесс незатухающих свободных колебаний в LC- контуре. Внешне оно полностью эквивалентно уравнению свободных колебаний груза на пружине в условиях отсутствующих сил трения. Аналогичный свободным механическим и электрическим колебаниям процесс изображен на рисунке 2.2.2. На данной иллюстрации приводятся графики зависимости заряда смещения x (t) груза и q (t) конденсатора от положения равновесия, а также графики изменений тока J (t) и скорости груза υ (t) за период T=2πω колебаний.

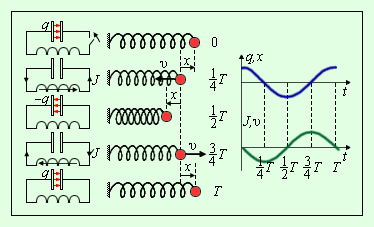
Рисунок 2.2.2.Аналогия процессов свободных электрических и механических колебаний.

Сделать заключение о некой связи между механическими и электрическими величинами нам позволяет сопоставление процессов в электрическом колебательном контуре и свободных колебаний груза на пружине. Данные аналогии показаны в таблице.

Электрические величины	Механические величины
Заряд конденсатора	q (t)	Координата	x(t)
Ток в цепи	J=dqdt	Скорость	ν=dxdt
Индуктивность	L	Масса	m
Величина, обратная электроемкости	1C	Жесткость	k
Напряжение на конденсаторе	U=qC	Упругая сила	kx
Энергия электрического поля конденсатора	q22C	Потенциальная энергия пружины	kx22
Магнитная энергия катушки	LI22	Кинетическая энергия	mν22
Магнитный поток	LI	Импульс	mυ

Колебания в последовательном RLC-контуре при воздействии в виде отрезка гармонического колебания

Задача 19.4.

Пусть при нулевых начальных условиях на последовательный RLC-контур, имеющий резонансную частоту действует отрезок гармонического колебания с той же частотой

Найти закон изменения тока в контуре.

Решение. Запишем ток в операторной форме согласно закону Ома:

и подставим сюда изображение воздействия

и операторное сопротивление контура

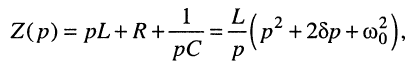
где

— коэффициент затухания контура,

— резонансная частота.

В результате получаем сложную функцию

(9.13)

не имеющую табличного соответствия. Для определения оригинала представим (19.13) в виде суммы простых дробей:

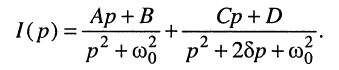(19.14)

Коэффициенты А, В, С, D определим методом неопределённых коэффициентов, как это было сделано в разд. 19.3.3, для чего приведём дроби (19.14) к общему знаменателю и приравняем числители новой дроби числителю (19.13). После этих несложных преобразований получаем равенство

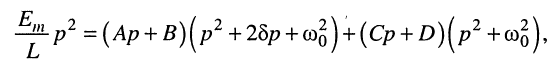
которое, как нетрудно видеть, справедливо при следующих соотношениях между коэффициентами:

Решение этой системы линейных уравнений даёт:

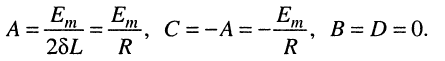
Подставляя коэффициенты в (19.14), имеем:

Оригиналы для дробей, стоящих в скобках, известны (см. табл. 16.1), и можно сразу записать выражение для тока:

(19.15)
где

— частота собственных затухающих колебаний контура с потерями.

Выражение для тока (19.15) существенно упрощается, если учесть, что на практике применяются контуры высокой добротности для которых

При этих условиях выражение для тока принимает вид:

(19.16)

Функция (19.16) описывает колебание (рис. 19.10), которое отличается от гармонического воздействия тем, что его амплитуда возрастает по экспоненциальному закону, стремясь к значению

которое принято называть установившимся.

Из (19.16) следует, что нарастание амплитуды тока происходит тем быстрее, чем больше коэффициент затухания контура 5. Напомним, что процесс установления колебаний в контуре происходит за время

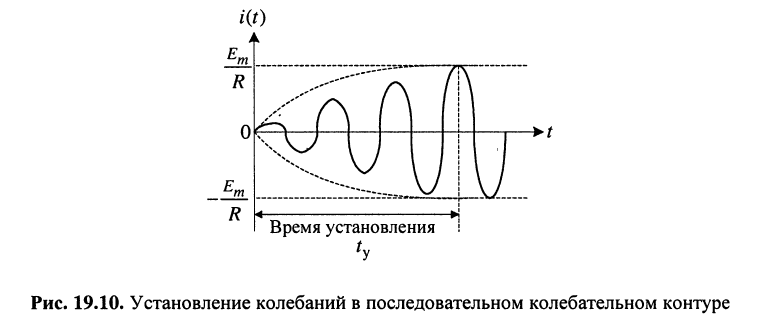
Найдём связь между длительностью переходного процесса и шириной полосы пропускания контура, для чего подставим в формулу для значение

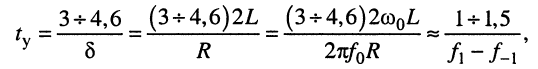
откуда полагают, что
(19.17)

Выводы:

чем выше добротность контура, т. е. чем уже его полоса пропускания, тем больше длительность переходного процесса, а это, в свою очередь, приводит к большим искажениям формы передаваемого сигнала;
произведение полосы пропускания контура на длительность переходного процесса в контуре согласно (19.17) приближённо равно единице ; это справедливо и для более сложных избирательных цепей.

Собственные колебания контура

Определение 2

Если системе в начальный момент времени сообщили определенное количество энергии, то она начинает совершать собственные колебания.

Важно, что постоянный источник ЭДС при этом отсутствует. Определение 3

Определение 3

Если собственные колебания вызваны наличием только квазиупругой силы, то они являются гармоническими.

Пример 1

Возьмем для примера ситуацию, когда в колебательном контуре отсутствует источник ЭДС. В таком случае уравнение колебательного контура можно записать в следующем виде:

d2Idt2+ω2I=.

Решить уравнение можно, описав свободные колебания при сопротивлении, входящем в состав контура:

I(t)=e-βt(Acos ωt+Bsin ωt).

Здесь может быть указан косинус вместо синуса. В обоих случаях это будет верно, поскольку обе функции имеют соответствующий сдвиг. Если R>2LC, то изменения заряда нельзя считать колебаниями. Если β=, то колебания в цепи становятся свободными. Если же β> и потери энергии на сопротивление незначительны, то такие колебания будут гармоническими.

Определение 4

Заряд конденсатора, изменения которого нельзя считать колебаниями, называется апериодическим.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

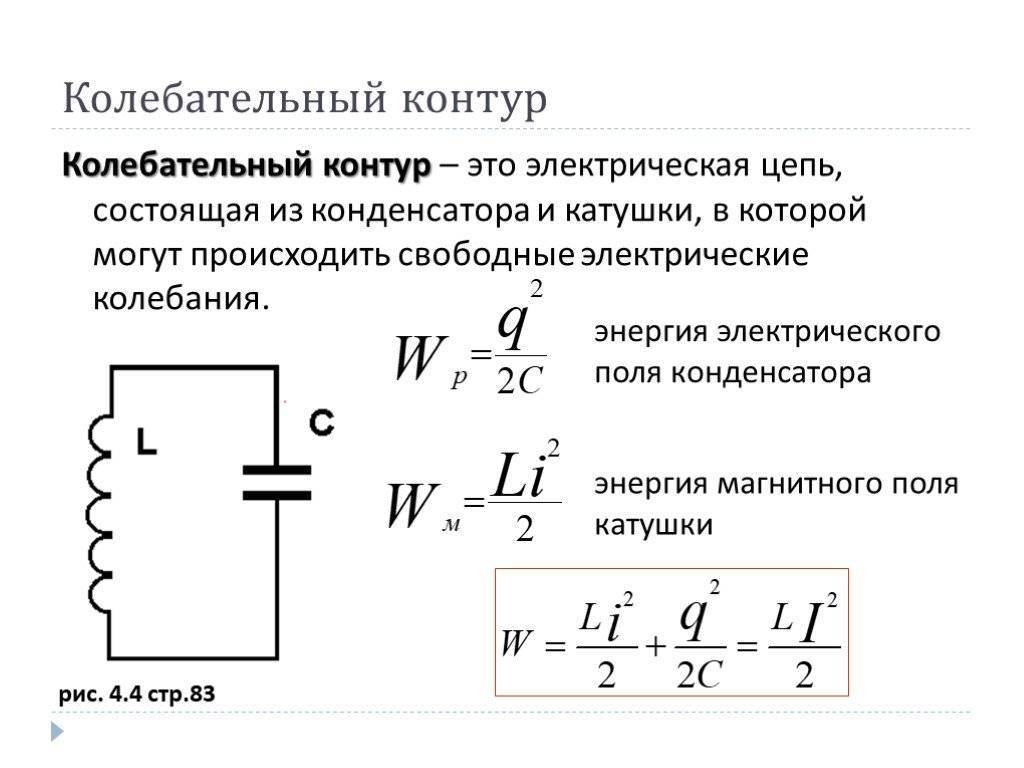
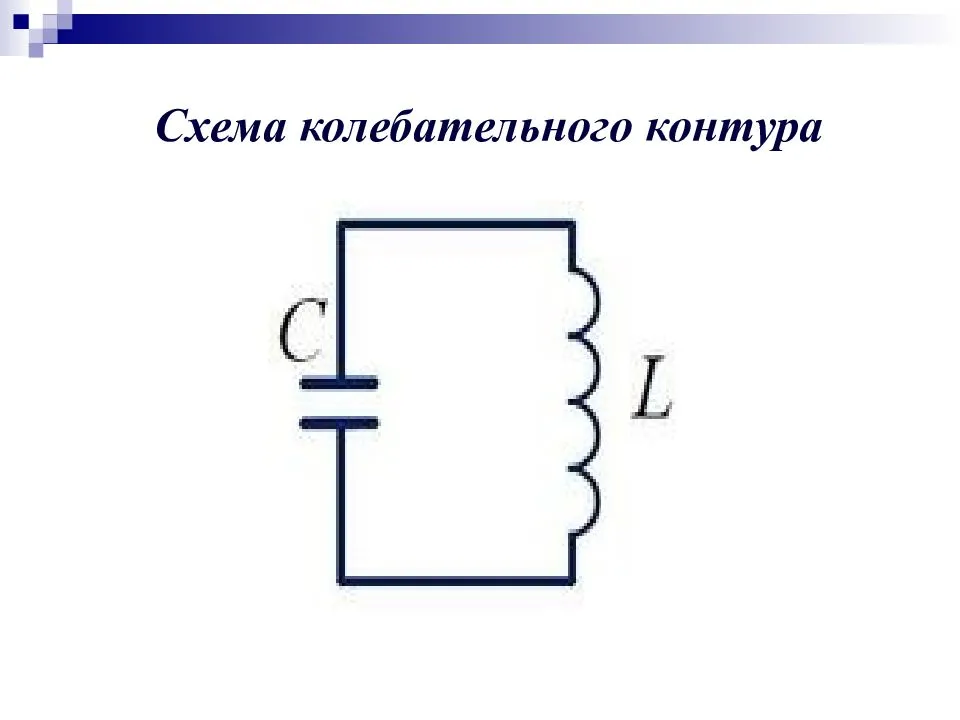
Что такое колебательный контур, из каких элементов состоит

Колебательный контур является простейшей системой, для которой характерно образование свободных электромагнитны колебаний.

Колебательный контур представляет собой электрическую сеть. В состав замкнутого контура входят следующие компоненты:

конденсатор;
катушка;
резистор.

В цепи образуются свободные затухающие колебания электромагнитного характера. В зависимости от силы сопротивления резистора определяется скорость затухания колебаний.

Идеальным колебательным контуром называют колебательный контур с полным отсутствием электрического сопротивления. Для такой системы характерны незатухающие свободные электромагнитные колебания.

Области применения резонансных контуров достаточно широки. Они необходимы для изготовления полосовых и режекторных фильтров в усилителях, радиоприемниках и устройствах автоматики.

Комплексное сопротивление (импеданс) колебательного контура

Колебательный контур может быть рассмотрен как двухполюсник, представляющий собой параллельное включение конденсатора и катушки индуктивности. Комплексное сопротивление такого двухполюсника возможно записать как

где i — мнимая единица.

Для такого двухполюсника имеет право быть быть определена т. н. характеристическая частота (или резонансная частота), когда импеданс колебательного контура стремится к бесконечности (знаменатель дроби стремится к нулю).

Эта частота равна

и совпадает по значению с собственной частотой колебательного контура.

Из этого уравнения следует, что на одной и той же частоте может работать множество контуров с разными величинами L и C, но с одинаковым произведением LC.

Математическое описание процессов

Напряжение, возникающее в катушке при изменении протекающего тока равно

Аналогично для тока, вызванного изменением напряжения на конденсаторе:

Поскольку всё возникающее в катушке напряжение падает на конденсаторе, то , а ток, вызванный конденсатором проходит через катушку, то . Дифференцируя одно из уравнений и подставляя результат в другое, получаем

Это уравнение гармонического осциллятора с циклической частотой (иначе она называется собственной частотой гармонического осциллятора)

Решением такого уравнения является

где — некая постоянная, называемая амплитудой колебаний, — также некоторая постоянная, называемая начальной фазой. И, например, при начальных условиях решение сведётся к

Решение может быть записано также в виде

где и — некоторые константы, которые связаны с амплитудой и фазой следующими отношениями

Закон сохранения энергии в колебательном контуре, формула

Рассмотреть колебательный контур можно на примере идеальной модели с конденсатором, емкость которого обозначается $С$, и катушкой, характеризующейся индуктивностью $L$. Исходя из особенностей идеального контура, в нем отсутствуют потери энергии. Во время колебательных движений энергия электрического поля $WC$ преобразуется в энергию магнитного поля $WL$ и наоборот. Представить этот процесс можно в виде формулы:

$W = WC(t) + WL(t) = const$

Максимального значения энергия достигает при максимальном значении заряда $q$. Данное соотношение можно представить с помощью уравнения:

$W_{Cmax}= \frac{q^{2}max}{2C}$

В этом случае наблюдается нулевое значение энергии магнитного поля в катушке индуктивности, то есть ток равен нулю.

Для того чтобы весь объем электрической энергии трансформировался в энергию магнитного поля, необходимо иметь в контуре ток $I$ максимального значения. Данное отношение описывается формулой:

$W_{Lmax}= \frac{LI^{2}max}{2}$

Тогда энергия электрического поля и заряд на конденсаторе будут равны нулю.

При таких условиях можно вывести следующее соотношение:

$W_{Lmax}= \frac{LI^{2}max}{2}= \frac{q^{2}max}{2C}= W_{Cmax}$

$Imax = ωqmax$

Резонанс токов

Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:

Чему будет равняться резонансный ток Iрез ? Считаем по закону Ома:

Iрез = Uген /Rрез , где Rрез = L/CR.

Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток Iкон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.

Автоколебания

Незатухающие вынужденные колебания поддерживаются в цепи действием внешнего периодического напряжения. Но существует способ создания незатухающих колебаний, при котором колебательная система сама регулирует поступление энергии в колебательный контур для компенсации потерь энергии на резисторе.

Определения

Автоколебательные системы — системы, в которых генерируются незатухающие колебания за счет поступления энергии от источника тока внутри системы.

Автоколебания — незатухающие колебания, существующие в системе без воздействия на нее внешних периодических сил.

Самый простой пример автоколебательной системы — это генератор на транзисторе. Транзистор представляет собой полупроводниковое устройство, состоящее из эмиттера, базы и коллектора и имеющее 2 p–n перехода. Колебания тока в контуре вызывают колебания напряжения между эмиттером и базой, которые, в свою очередь, управляют силой тока в цепи колебательного контура (обратная связь). От источника напряжения в контур поступает энергия, компенсирующая потери энергии в контуре на транзисторе.

Схема автоколебательной системы представлена ниже.

Преимуществом такой схемы является то, что конденсатор при этом подключается к источнику тока только тогда, когда присоединенная к положительному источнику тока пластина конденсатора заряжена положительно (рис. а). Только в этом случае конденсатор восполняет потери энергии, выделенной на резисторе.

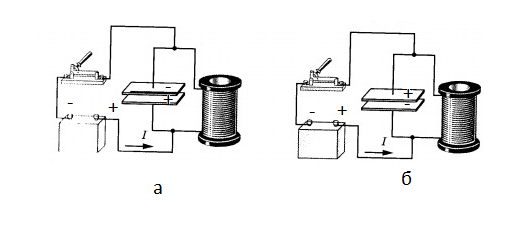
Если бы источник тока был включен всегда, восполнения потерь не происходило бы. Поскольку конденсатор разряжался бы в момент, когда он соединен с источником тока пластиной, заряженной отрицательно (рис. б).

Радиолюбитель

Практический расчет последовательного или параллельного LC контура.

Доброго дня уважаемые радиолюбители! Сегодня мы с вами рассмотрим порядок расчета LC контура.

Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. К примеру, очень многие начинающие радиолюбители (естественно, в основном молодые), увлекаются сборкой так называемых “жучков” – устройств позволяющих на расстоянии прослушивать что-нибудь. Конечно я уверен, что это делается без всяких нехороших (даже грязных) мыслей подслушать кого-нибудь, а в благих целях. Например устанавливают “жучок” в комнате с малышом, а на радиовещательный приемник прослушивают не проснулся ли он. Все схемы “радиожучков” работают на определенной частоте, но что делать, когда эта частота вас не устраивает. Вот тут вам придет на помощь знание нижеприведенной статьи.

LC колебательные контура применяются практически в любой аппаратуре, работающей на радиочастотах. Как известно из курса физики, колебательный контур состоит из катушки индуктивности и конденсатора (емкости), которые могут быть включены параллельно (параллельный контур) или последовательно (последовательный контур), как на рис.1:

Реактивные сопротивления индуктивности и емкости, как известно, зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости – падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. Таким образом, для каждого контура есть некоторая частота резонанса, на которой индуктивное и емкостное сопротивления оказываются равными. В момент резонанса резко увеличивается амплитуда переменного напряжения на параллельном контуре или резко увеличивается амплитуда тока на последовательном контуре. На рис.2 показан график зависимости напряжения на параллельном контуре или тока на последовательном контуре от частоты:

На частоте резонанса эти величины имеют максимальное значение. А полоса пропускания контура определяется на уровне 0,7 от максимальной амплитуды, которая есть на частоте резонанса.

Теперь перейдем к практике. Предположим нам нужно сделать параллельный контур, имеющий резонанс на частоте 1 МГц. Прежде всего нужно сделать предварительный расчет такого контура. То есть, определить необходимую емкость конденсатора и индуктивность катушки. Для предварительного расчета есть упрощенная формула:

L=(159,1/F)2/C где: L – индуктивность катушки в мкГн; С – емкость конденсатора в пФ; F – частота в МГц

Зададимся частотой 1 МГц и емкостью, к примеру, 1000 пФ. Получим:

L=(159,1/1)2 /1000 = 25 мкГн

Таким образом, если мы захотим контур на частоту 1 МГц, то нужен конденсатор на 1000 пФ и индуктивность на 25 мкГн. Конденсатор можно подобрать,, а вот индуктивность нужно сделать самостоятельно.

Рассчитать число витков для катушки без сердечника можно по такой формуле:

N=32 *√(L/D) где: N – требуемое число витков; L – заданная индуктивность в мкГн; D – диаметр каркаса в мм, на котором предполагается намотать катушку.

Предположим, диаметр каркаса – 5 мм, тогда:

N=32*√(25/5) = 72 витка.

Данная формула является приближенной, она не учитывает собственную межвитковую емкость катушки. Формула служит для предварительного вычисления параметров катушки, которые затем настраиваются при настройке контура.

В радиолюбительской практике чаще используются катушки с подстроечными сердечниками из феррита, имеющими длину 12-14 мм и диаметр 2,5 – 3 мм. Такие сердечники, например, применяются в контурах телевизоров и приемников. Для предварительного расчета числа витков для такого сердечника есть другая приближенная формула:

N=8,5*√L , подставляем значения для нашего контура N=8,5*√25 = 43 витка. То есть, в таком случае на потребуется намотать на катушку 43 витка провода.

Принцип работы

Принцип работы контура состоит в поочередном обмене электрической энергией между элементами емкости и индуктивности. Происходит превращение емкостной в индуктивную и обратно. Процессы следует рассмотреть подробнее. Для этого нужно зарядить конденсатор до величины напряжения Uc. Энергия будет определяться по формуле Wс = (C * U2) / 2. Если к конденсатору подсоединить катушку индуктивности, то это вызовет в ней ЭДС самоиндукции.

При этом энергия электромагнитного поля станет рассчитываться по такому соотношению: Wl = (L * I2) / 2. Из-за нее будет постепенно уменьшаться ток в электрической цепи контура. Векторы токов конденсатора и катушки направлены в разные стороны. Следовательно, они компенсируют друг друга по I закону Кирхгофа и не выходят за пределы системы.

Циклическая частота гармонических колебаний

Колебательные движения играют важную роль в самых разных вопросах физики. Рассмотрим колебания материальной точки. При колебаниях материальная точка через равные промежутки времени проходит через одно и то же положение при движении в одном направлении.

Самым важным колебательными движениями являются гармонические колебания. Сущность таких колебаний проще всего рассмотреть на следующей кинематической модели. Путь точка M со скоростью ($v$) постоянной по величине движется по окружности радиуса A. При этом ее угловая скорость равна $_0=const$ (рис.1).

Проекция точки на диаметр окружности, например на ось X, совершает колебания от $N_1$ до $N_2 $и обратно (точка N). Такое колебание N ,будет называться гармоническим. Для его описания следует записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол $_0$. Через некоторый промежуток времени этот угол получит приращение $_0t$ и станет равен $_0t+_0$, тогда:

Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.

Рассмотрим формулу (1). Параметр $A$ – максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О – центра окружности), амплитуда колебаний.

Величина $_0$ – циклическая частота колебаний. $varphi =(_0t+_0$) – фаза колебаний; $_0$ – начальная фаза колебаний. Циклическую частоту гармонических колебаний определим как частную производную от фазы колебаний по времени:

Применение колебательных контуров

Хорошим примером применения силовых последовательного и параллельного колебательных контуров является силовой резонансный фильтр для получения синусоидального напряжения

Еще интересные схемы:

(А), (Б), (В) — фильтры сигнала заданной частоты, (Г) — фильтр-пробка, (Д) — входная цепь радиоприемника, (Е) — стабилизатор переменного напряжения. Катушка L2 специально сделана насыщающейся при некотором нужном переменном напряжении на ней, что обеспечивает поддержание этого выходного напряжения по форме близкого к синусоиде.

(читать дальше…) :: (в начало статьи)

:: ПоискТехника безопасности :: Помощь

К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.

Если что-то непонятно, обязательно спросите!Задать вопрос. Обсуждение статьи. сообщений.

Позвольте не согласиться с вашим выражением (Если последовательный колебательный контур не был запитан, а теперь на него подали синусоидальный сигнал резонансной частоты, то сопротивление будет уменьшаться постепенно, по мере перехода контура в стационарный режим работы). Что означает ‘постепенно’? Читать ответ…

Насколько я помню в контуре (и последовательном, и в параллельном) на резонансной частоте сопротивление носит активный характер, вы же при рассмотрении параллельного контура допустили выражение реактивное сопротивление контура на резонансной частоте. На частотах ниже резонансной (в параллельном контуре) сопротивление носит индуктивный характер, на частотах выше резонансной соп Читать ответ…

Еще статьи

Расчет дросселя, катушки индуктивности. Рассчитать, посчитать онлайн, …
Форма для онлайн расчета дросселя, катушки индуктивности. Для изготовления индук…

Практика проектирования электронных схем. Самоучитель электроники….
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы….

Резонансный инвертор, преобразователь напряжения повышающий. Схема, ко…
Инвертор 12/24 в 300. Резонансная схема….

Силовой резонансный фильтр для получения синусоиды от инвертора…
Для получения синусоиды от инвертора нами был применен самодельный силовой резон…

Генератор синусоидального напряжения, сигнала, синуса, синусоиды. Гир…
Расчет гиратора и генератора синусоидального сигнала на нем….

Металлоискатель самодельный. Сделать, собрать самому, своими руками. С…
Схема металлоискателя с высокой разрешающей способностью. Описание сборки и нала…

Блокинг генератор. Схема, устройство….
Схема и устройство блокинг генератора…

Индуктивность. Генри. Henry. Гн. Единицы измерения. Доли, миллигенри, …
Понятие индуктивности. Единицы измерения. Катушки индуктивности….

Свойства электромагнитных волн

Электромагнитная волна – это изменяющееся во времени и распространяющееся в пространстве электромагнитное поле.

Существование электромагнитных волн было теоретически предсказано английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны были открыты Г. Герцем.

Источник электромагнитной волны – ускоренно движущаяся заряженная частица – колеблющийся заряд.

Важно! Наличие ускорения – главное условие излучения электромагнитной волны. Интенсивность излученной волны тем больше, чем больше ускорение, с которым движется заряд

Источниками электромагнитных волн служат антенны различных конструкций, в которых возбуждаются высокочастотные колебания.

Электромагнитная волна называется монохроматической, если векторы $ \vec{E} $ и $ \vec{B} $ совершают гармонические колебания с одинаковой частотой (частотой волны).

Длина электромагнитной волны: $ \lambda=cT=\frac{c}{\nu}, $

где $ c $ – скорость электромагнитной волны, $ T $ – период, $ \nu $ – частота электромагнитной волны.

Свойства электромагнитных волн

В вакууме электромагнитная волна распространяется с конечной скоростью, равной скорости света 3·108 м/с.
Электромагнитная волна поперечная. Колебания векторов напряженности переменного электрического поля и магнитной индукции переменного магнитного поля взаимно перпендикулярны и лежат в плоскости, перпендикулярной к вектору скорости волны.
Электромагнитная волна переносит энергию в направлении распространения волны.

Важно! Электромагнитная волна в отличие от механической волны может распространяться в вакууме. Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени

Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени.

Обозначение – $ I $, единица измерения в СИ – ватт на квадратный метр (Вт/м2).

Важно! Плотность потока излучения электромагнитной волны от точечного источника убывает обратно пропорционально квадрату расстояния от источника и пропорциональна четвертой степени частоты. Электромагнитная волна обладает общими для любых волн свойствами, это:

Электромагнитная волна обладает общими для любых волн свойствами, это: