Линии напряженности электрического поля

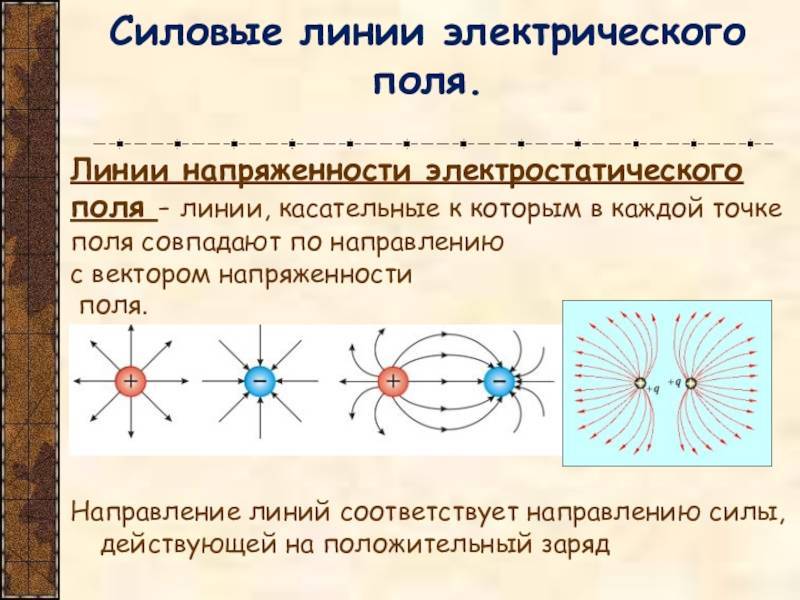
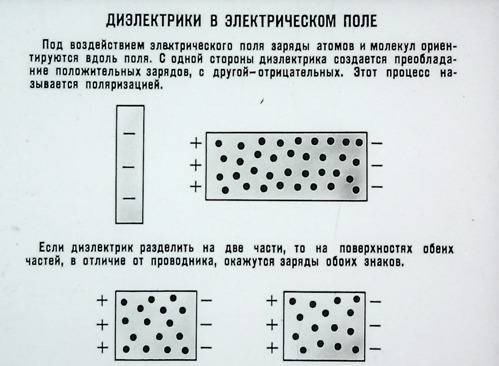
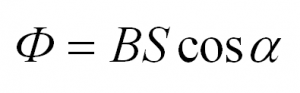Силовые линии электрического поля.

Электрическое поле в пространстве принято представлять силовыми линиями. Понятие о силовых линиях ввел М. Фарадей при исследовании магнетизма. Затем это понятие было развито Дж. Максвеллом в исследованиях по электромагнетизму.

Силовая линия, или линия напряженности электрического поля, — это линия, касательная к которой и каждой ее точке совпадает с направлением силы, действующей на положительный точечный заряд, находящийся в этой точке поля.

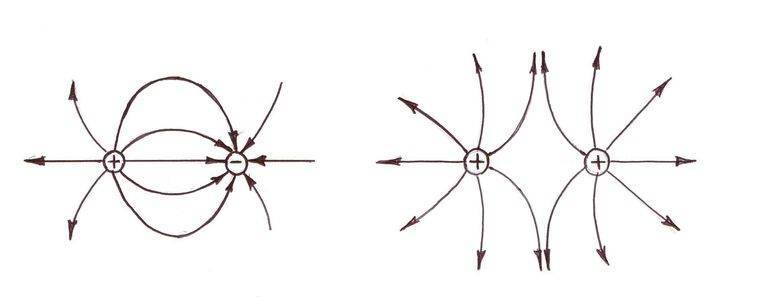
На рисунках ниже изображены линии напряженности положительно заряженного шарика (рис. 1); двух разноименно заряженных шариков (рис. 2); двух одноименно заряженных ша­риков (рис. 3) и двух пластин, заряженных разными по знаку, но одинаковыми по абсолютной величине зарядами (рис. 4).

Линии напряженности на последнем рисунке почти параллельны в пространстве между пластинами, и плотность их одинакова. Это говорит о том, что поле в этой области пространства одно­родно. Однородным называется электрическое поле, напряженность которого одинакова во всех точках пространства.

В электростатическом поле силовые линии не замкнуты, они всегда начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Они нигде не пересекаются, пересе­чение силовых линий говорило бы о неопределенности направления напряженности поля в точке пересечения. Плотность силовых линий больше вблизи заряженных тел, где напряженность поля больше.

Взаимодействие зарядов передается без участия вещества

Заряды будут притягиваться и отталкиваться не только в воздухе, но, даже в безвоздушном пространстве. В этом легко убедиться, если поместить заряженный электроскоп под колокол и откачать из-под колокола воздух. Полоски бумаги, имеющие одинаковые заряды, все так же, продолжат отталкиваться, независимо от того, в воздухе ли они находятся, либо в безвоздушном пространстве.

Рис. 2. Для передачи взаимного действия зарядов вещество не нужно, так как это взаимодействие передается не через вещество

Это значит, что передача взаимодействия зарядов происходит не через вещество.

Ученые из Англии – Майкл Фарадей и Джеймс Максвелл, долгое время изучали электрические заряды. Они выяснили, что заряды окружены особым видом материи, которую они назвали электрическим полем.

Общие сведения

Неким фундаментальным свойством природы является электрический заряд. Один из разделов физики занимается изучением его свойств и взаимодействия, называется он электродинамикой. Наиболее интересно для учёных изучение влияния друг на друга заряженных тел.

Бум исследования электрических явлений пришёлся на XIX век. В это время появилось две теории, одна из которых оказалась ошибочной и была опровергнута экспериментами. Эта догадка называлась правилом дальнодействия. Согласно ей один заряд непосредственно действует на другой. То есть чем больше расстояние между взаимодействующими телами, тем меньше сила действия.

Но на самом деле электрические заряды влияют друг на друга по-другому. Эта теория получила название «Правило близкодействия». Как оказалось, если взять два заряженных тела, например, положительно, то первый заряд на второй не действует. Он просто изменяет вокруг себя пространство, создавая нечто. Эта материя и получила название «Электрическое поле». Именно оно и воздействует на второе тело. Другими словами, на заряд действует материя, создаваемая первой частицей. При этом распространяется она с довольно большой, но конечной, скоростью.

Опыты, проводимые Фарадеем, показали, что если из системы убрать одно из тел, то сила, действующая на вторую частицу, не изменится мгновенно, хотя это и произойдёт довольно скоро. Именно Фарадей и является открывателем электромагнитного поля. В дальнейшем Максвелл смог описать явление теоретически.

Электрическое поле можно обнаружить, поместив в неё другой заряд, и исследовать действие наблюдающийся силы. Электромагнитную материю можно описать количественно, поэтому, зная характеристики поля и заряда, можно определить величину силы.

К основным параметрам электростатического поля, то есть материи, созданной неподвижной частицей в пространстве, относят:

• напряжённость;
• потенциал.

Таким образом, если есть система заряженных тел, то в любой её точке будет существовать силовое электрическое поле. Его можно исследовать через силу, действующую на заряд, находящийся в этой материи.

Теории дальнодействия и близкодействия

Физики выдвигали различные теории, пытаясь объяснить взаимодействие зарядов. Наибольшее распространение получили две – их называют теориями близкодействия и дальнодействия.

Дальнодействие

Теория дальнодействия сообщает, что один заряд действует на другой заряд непосредственно. То есть, чтобы передать действие одного заряда на другой, посредники не нужны.

Кроме того, взаимодействие происходит мгновенно на любых расстояниях. Это значит, что если убрать один из взаимодействующих зарядов, то его действие на оставшийся заряд прекратится мгновенно.

Близкодействие

В противоположность этой теории Майкл Фарадей предложил свою теорию близкодействия.

Эта теория заявляет о том, что непосредственно действовать друг на друга заряды не могут. То есть, для передачи своего воздействия заряду нужна некоторый помощник. И каждый заряд создает в пространстве вокруг себя этого помощника. Фарадей назвал его электрическим полем.

На другие заряды будет действовать не сам заряд, а поле, созданное этим зарядом. Такое поле распространяется в пространстве не мгновенно, а с конечной скоростью.

Примечание: Как выяснилось позже, это очень большая скорость – триста тысяч километров в секунду. Ее называют скоростью света.

Поэтому, если один из взаимодействующих зарядов быстро убрать, то второй заряд узнает о его исчезновении не мгновенно, а через некоторое, пусть небольшое, время.

Получается, что взаимодействие зарядов протекает не непосредственно, а в виде цепочки. Каждый заряд создает вокруг себя поле, именно поле действует на другой заряд, помещенный в него.

А сила, действующая на заряд, расположенный в какой-либо точке пространства, зависит от характеристик поля в этой точке.

Рис. 3. Основные отличия теории дальнодействия от теории близкодействия

В настоящее время общепринятой теорией, объясняющей взаимодействие зарядов, является теория близкодействия Фарадея. Так как эта теория полностью подтвердилась экспериментально.

Примечание: Кроме электрических существуют, так же, магнитные поля. В отличие от электростатического, магнитное поле не имеет своих магнитных источников. Оно возникает в пространстве вокруг движущихся зарядов. То есть, магнитное поле – это поле электрических зарядов, находящихся в движении.

Джеймс Клерк Максвелл в середине 19-го века показал, что электрическое и магнитное поля связаны и это электромагнитное поле распространяется в пространстве с очень большой, но конечной скоростью.

Поле и вещество – это два вида материи

Мир, окружающий нас, материален. Значит, материя – это то, что существует реально, независимо от того, наблюдаем ли мы за ней, или нет.

Она может проявлять себя в виде двух частей — вещества и поля. Нас окружает вещество, а атомы и молекулы — это мельчайшие единицы вещества.

Поле – это еще один вид материи. Поле веществом не является, однако, оно существует реально.

Рис. 4. Материя состоит из двух частей — поля и вещества

§ 19. Напряжённость электростатического поля. Принцип суперпозиции

Для изучения свойств электростатического поля удобно использовать такую его характеристику, которая не зависит от числового значения пробного заряда и позволяет определить силу, действующую на заряд со стороны поля в любой его точке. Для гравитационного поля такой характеристикой, не зависящей от массы тела, является ускорение свободного падения . Какая физическая величина является характеристикой электростатического поля?

Напряжённость электростатического поля. Пусть электростатическое поле создано в вакууме точечным зарядом Q > 0. Если в некоторую точку поля поместить пробный положительный заряд q, на него будет действовать кулоновская сила отталкивания, модуль которой .

Сила не может служить характеристикой поля, так как её модуль пропорционален значению пробного заряда q. Однако отношение модуля силы, которой электростатическое поле точечного заряда Q действует на пробный заряд q, не зависит от значения пробного заряда:

(19.1)

и, следовательно, может служить характеристикой поля.

Эту характеристику называют напряжённостью электростатического поля и обозначают . Напряжённость характеризует силовое действие поля на вносимые в него заряды.

Напряжённость электростатического поля — физическая векторная величина, равная отношению силы, которой поле действует на пробный заряд, к значению этого заряда:

(19.2)

С учётом выражений (19.1) и (19.2) можно определить модуль напряжённости электростатического поля, созданного точечным зарядом Q, в точке, находящейся на расстоянии r от него:

Таким образом, модуль напряжённости поля, создаваемого в вакууме точечным зарядом, прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости.

Если заряд Q находится в однородной среде с диэлектрической проницаемостью ε, то модуль напряжённости поля .

Из выражения  следует, что единицей напряжённости электростатического поля в СИ является ньютон на кулон . В СИ широко используют другое название этой единицы — вольт на метр .

Зная напряжённость электростатического поля, можно определить силу, действующую на любой точечный заряд в любой точке этого поля:

(19.3)

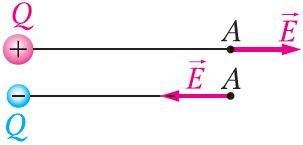Рис. 104

Напряжённость поля, как и сила, величина векторная. Направление напряжённости поля совпадает с направлением силы, действующей на положительный пробный электрический заряд. Напряжённость в любой точке электростатического поля точечного заряда направлена вдоль прямой, соединяющей эту точку и точечный заряд, создающий поле. Напряжённость поля, созданного точечным положительным зарядом Q > 0, направлена от заряда, а напряжённость поля, созданного точечным отрицательным зарядом Q < 0, — к заряду (рис. 104).

От теории к практике

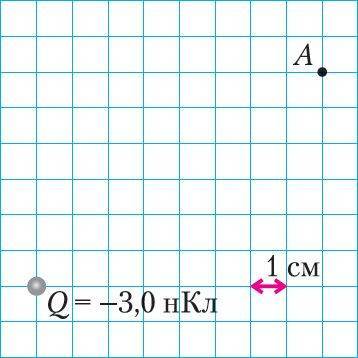Рис. 105

1. Как изменится модуль напряжённости в некоторой точке поля, созданного точечным зарядом Q, если: а) расстояние r от заряда до этой точки увеличить вдвое; б) заряд Q увеличить вдвое, а расстояние r от заряда до этой точки уменьшить вдвое?

2. Как направлена в точке А напряжённость поля, созданного неподвижным точечным зарядом (рис. 105)? Чему равен модуль напряжённости поля в этой точке?

Рис. 105.1

Модуль напряжённости поля уединённой проводящей сферы радиусом R, заряд которой Q (рис. 105.1), в точках на её поверхности r = R и вне сферы на расстоянии r > R от её центра определяют по формуле . В точках, находящихся внутри проводящей сферы r < R, напряжённость равна нулю , если внутри этой сферы нет электрических зарядов.

Напряжённость электростатического поля, создаваемого равномерно заряженной бесконечной плоскостью, одинакова во всех точках полупространства с каждой стороны от плоскости (при этом ), а её модуль

где S — площадь некоторого участка плоскости, — модуль заряда этого участка (рис. 105.2).

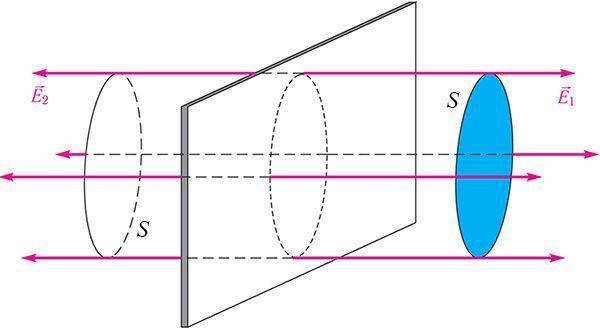Рис. 105.2

Интересно знать

Кроме гравитационного поля у Земли есть электрическое и магнитное поля. Модуль напряжённости электрического поля у поверхности Земли в среднем составляет . Электрическое поле Земли меняется во времени. Избыточный отрицательный электрический заряд земного шара колеблется около –6 · 105 Кл.

«Материальные уравнения»

Для решения многих практических задач вполне достаточна ограниченная точность. С помощью «материальных» уравнений выполняют расчеты различных электрических цепей.

Уместный пример – закон Ома. Он был создан в ходе измерения электрических параметров. В начальном виде формула (Х=П/L+B) состояла из следующих компонентов:

• Х – показания измерительного устройства (гальванометра), включенного в разрыв электрической цепи;
• П – параметры источника питания, заставляющие стрелку прибора отклоняться на определенный угол;
• L – длина соединительных проводов;
• B – общие свойства установки.

Несложно догадаться, что в современном представлении это известный закон, показывающий взаимное влияние основных параметров полной электрической цепи:

I = E/R+r,

где:

• I – ток;
• E – ЭДС (напряжение);
• R и r – сопротивление подключенных компонентов и самого источника питания, соответственно.

Электростатика

Этот раздел электродинамики описывает частный случай, когда заряженные тела находятся в статичном состоянии. Такая ситуация значительно упрощает расчеты. Для практического примера можно создать электростатический конденсатор.

Устанавливают две плоскости одинаковой размерности параллельно на небольшом расстоянии, разделяют слоем диэлектрика. Если создать разницу потенциалов, между поверхностями образуется поле. В такой конструкции накапливается электрический заряд. Какой будет емкость, можно узнать с помощью этой формулы:

C=Q/ (ϕ1-ϕ2)=Q/U=e*S/d,

где

• e – проницаемость диэлектрика;
• e0 – электрическая постоянная (8,85*10-12 Ф/м);
• S – площадь пластин;
• D – расстояние между ними.

Конденсатор

Чтобы зарядить конденсатор до нужной емкости, надо затратить энергию W=(e*e0*E2/2)*S*D. На рисунке показано, как изменять рабочие параметры сборки при последовательном и параллельном соединении модулей.

Теорема Гаусса

Эта теорема определяет пропорциональность потока вектора напряженности электрического поля (Ф) заряду (Q), который заключен в произвольную поверхность замкнутого типа:

Ф=4π*Q.

Напряжённость электрического поля точечного заряда

В этом случае можно пользоваться рассмотренным выше законом Кулона. В следующих разделах представлены формулы для вычисления в разных системах единиц.

В единицах СИ

В этой системе базовой выбрана сила тока, поэтому кулон является производной величиной.

Основная формула:

F=k*(q1*q2/r122).

Здесь коэффициент k=1/(4π*e0).

Для системы СГС

Здесь, как и в предыдущем примере, выбран единичный заряд – «точка». Основные правила характеризуют физические процессы аналогично. Разница лишь в постоянных величинах. В данном случае коэффициент k обратно пропорционален диэлектрической проницаемости (е) среды.

В этом варианте для получения результата надо сложить вектора каждого заряда:

Еобщ=Е1+Е2+…+En.

Чтобы обеспечить непрерывность линии напряженности, берут интеграл соответствующей области. Построить распределение силовых линий можно с помощью расчета перемещения вектора по всем точкам.

Физика распространения

Если рассматривать одинокую частицу, то линии силы будут исходить от неё в радиальном направлении. При взаимодействии же двух и более зарядов на вид распространения влияет напряжённость. Чтобы нарисовать, как будут выглядеть линии, следует сложить векторы напряжённости. Их результирующая и будет характеризовать суммарное поле.

При составлении картинки распространения поля нужно учитывать, что точки соприкосновения на силовой линии определяются вектором напряжённости. Чтобы математически описать силовые кривые, необходимо составить уравнения. Вектора в них будут являться производными первого порядка. По сути, это обыкновенные касательные.

Каждая частица, добавленная в электромагнитное поле, оказывает на него влияние. Соответственно будет изменяться и узор кривых сил. Но в любом случае основой для построения визуализированного рисунка будет вектор напряжённости каждого источника поля. При этом правило, что линии напряжённости начинаются на положительном заряде, а заканчиваются на отрицательном, условное.

Довольно интересным для изучения является процесс возникновения электрического поля между заряженными бесконечными плоскостями. Созданная однородная материя между пластинками будет распространяться в параллельном направлении, то есть линии пересекаться не будут. Если же в зазор между ними внести точечный заряд, то кривые начнут изгибаться по дуге, поле станет неоднородным, а значение напряжённости будет зависеть от плотности.

Распространение поля подчиняется следующим правилам:

• излучается во все направления;
• изменяет свой рисунок при оказании внешнего воздействия;
• уменьшается при удалении от источника;
• может быть как однородным, так и неоднородным.

Электрические силы при внесении заряженной частицы в поле совершают работу. При незначительном воздействии её можно описать так: A = F * l * cos (a) = E * q * L. Таким образом, структура распространения зависит от расстояния между частицами.

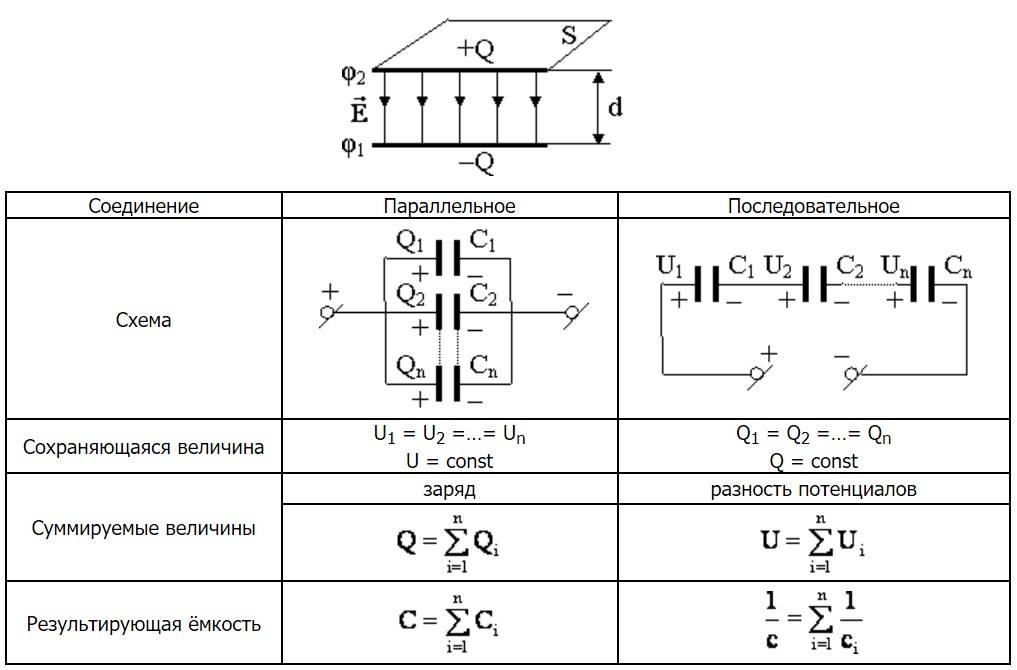
Электрическая емкость. Конденсатор

Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.

Обозначение – ​\( C \)​, единица измерения в СИ – фарад (Ф).

Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.

Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:

Формула для вычисления электроемкости:

где ​\( q \)​ – заряд проводника, ​\( \varphi \)​ – его потенциал.

Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.

Электроемкость конденсатора рассчитывается по формуле:

где ​\( q \)​ – модуль заряда одной из обкладок,
​\( U \)​ – разность потенциалов между обкладками.

Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.

Плоский конденсатор представляет две параллельные пластины площадью ​\( S \)​, находящиеся на расстоянии ​\( d \)​ друг от друга.

Электроемкость плоского конденсатора:

где ​\( \varepsilon \)​ – диэлектрическая проницаемость вещества между обкладками,\( \varepsilon_0 \) – электрическая постоянная.

На электрической схеме конденсатор обозначается:

Виды конденсаторов:

• по типу диэлектрика – воздушный, бумажный и т. д.;
• по форме – плоский, цилиндрический, сферический;
• по электроемкости – постоянной и переменной емкости.

Конденсаторы можно соединять между собой.

Параллельное соединение конденсаторов

При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:

Общая емкость:

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.

Заряды конденсаторов при таком соединении равны:

Общее напряжение:

Величина, обратная общей емкости:

При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.

Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости

Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.

Задачи на теорему Гаусса с решением

Если вам нужно сначала освежить теоретические знания, читайте подробную теорию по теореме Гаусса в нашем справочнике. Ну а перед решением задач не забудьте повторить памятку и на всякий случай держите под рукой полезные формулы.

Кстати, при решении задач на теорему Гаусса придется довольно часто брать интегралы. Хотите научиться делать это по-быстрому? У нас уже есть отдельная статья и видео на эту тему.

Задача на теорему Гаусса №1: напряженность поля плоскости

Условие

Определите напряженность поля бесконечной заряженной плоскости. Поверхностная плотность заряда сигма.

Решение

Линии напряженности перпендикулярны рассматриваемой плоскости и направлены в обе стороны от неё. Выберем в качестве гауссовой поверхности цилиндр с основанием, параллельным плоскости:

По теореме Гаусса:

Поток сквозь цилиндр равен сумме потоков сквозь боковую поверхность цилиндра и потокам сквозь оба его основания. Поток сквозь боковую поверхность равен нулю, так как линии напряженности параллельны ей:

Согласно теореме Гаусса:

Отсюда:

Ответ: см. выше.

Задача на теорему Гаусса №2: напряженность поля двух пластин

Условие

Электрическое поле создано двумя параллельными заряженными тонкими пластинами с поверхностными плотностями заряда + сигма  и -2 сигма. Площадь каждой пластины S, расстояние между пластинами d можно считать значительно меньшим их продольных размеров. Какова напряженность электрического поля, созданного этими пластинами?

Решение

Для электрического поля действует принцип суперпозиции: результирующее поле равно векторной сумме отдельных полей каждой пластины. Из предыдущей задачи мы знаем формулу, по которой вычисляется напряженность поля тонкой заряженной пластины, запишем для каждой из них:

Векторы напряженности между пластинами совпадают по направлению, результирующая напряженность равна:

Справа и слева от пластин, во внешней области, векторы направлены в разные стороны:

Для наглядности приведем рисунок:

Ответ: см. выше.

Задача на теорему Гаусса №3: напряженность электрического поля бесконечной нити

Условие

Определить напряженность электрического поля, создаваемую бесконечной тонкой нитью, равномерно заряженной с линейной плотностью заряда лямбда.

Решение

Напряженность будем искать при помощи теоремы Гаусса. Наша задача – определить зависимость напряженности от расстояния от нити. В качестве поверхности выберем цилиндр с боковыми стенками, параллельными нити. Будем учитывать только поток вектора напряженности через боковую поверхность, так как поток через основания цилиндра равен нулю:

Заряд нити внутри рассматриваемой поверхности равен заряду отрезка нити длиной l:

По теореме Гаусса:

Отсюда:

Ответ: см. выше.

Задача с применением теоремы Гаусса №4

Условие

Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределённым зарядом (τ = 10 нКл/м). Определить кинетическую энергию Т2 электрона в точке 2, если в точке 1 его кинетическая энергия Т1 = 200 эВ. Расстояние точки 2 от линии равно а = 0,5 см, точки 1 – b=1,5 см.

Решение

Ранее рассмотренные задачи были примерами вычисления полей с помощью теоремы Гаусса. Теперь рассмотрим задачу, которая решается сиспользованием этой информации. Из предыдущей задачи возьмем выражение для напряженности поля заряженной нити:

Разность потенциалов поля в двух точках будет равна:

При прохождении этой разницы потенциалов электрон приобретёт кинетическую энергию:

Конечная энергия частицы будет равна:

Получим:

Ответ: 397.6 эВ.

Задача на теорему Гаусса №5: поток электрического поля

Условие

Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найти поток вектора напряженности через круг радиуса R. Плоскость круга проходит через его середину и перпендикулярна отрезку прямой, соединяющей заряды.

Решение

Рассмотрим элементарный поток результирующего электрического поля через бесконечно малую кольцевую зону круга: 

В записи потока учтено, что вектор напряженности перпендикулярен поверхности круга. Выразим напряженность электрического поля через «ро», используя подобие треугольников, показанных на рисунке:

Вычисление потока сводится к взятию интеграла:

Ответ: см. выше.

Примеры применения теоремы Гаусса можно найти не только в электростатике, но и в других областях физики.

Электрическое поле

Рассмотренный ранее устанавливает количественные и качественные особенности взаимодействия точечных электрических зарядов в вакууме. Однако этот закон не дает ответа на весьма важный вопрос о механизме взаимодействия зарядов, т.е. посредством чего передается действие одного заряда на другой. Поиск ответа на этот вопрос привел английского физика М. Фарадея к гипотезе о существовании электрического поля, справедливость которой была полностью подтверждена последующими исследованиями. Согласно идее Фарадея электрические заряды не действуют друг на друга непосредственно. Каждый из них создает в окружающем пространстве электрическое поле. Поле одного заряда действует на другой заряд, и наоборот.

Все сказанное позволяет дать следующее определение:

электрическое поле – это особый вид материи, посредством которого осуществляется взаимодействие электрических зарядов.

Свойства электрического поля

Электрическое поле материально, т.е. существует независимо от наших знаний о нем.

Порождается электрическим зарядом: вокруг любого заряженного тела существует электрическое поле.
Поле, созданное неподвижными электрическими зарядами, называется электростатическим.
Электрическое поле может быть создано и переменным магнитным полем. Такое электрическое поле называется вихревым.

Обнаружить электрическое поле можно по действию его на электрические заряды с некоторой силой.

Электрическое поле распространяется в пространстве с конечной скоростью, равной скорости света в вакууме.
Таким образом, если один из взаимодействующих зарядов переместить в другую точку пространства, то второй заряд почувствует изменение положения первого заряда не мгновенно, а спустя некоторый промежуток времени \(~\Delta t = \dfrac{l}{c}\), где с — скорость света в вакууме, l — расстояние между зарядами.

Электрическая напряженность в быту

Вначале создается электрический потенциал для получения поля. Любой диэлектрик натирается о шерсть, волосы, используется, например, пластиковая ручка или эбонитовая палочка. На поверхности предмета создается потенциал, а вокруг возникает электрическое поле. Ручка с зарядом притягивает мелкие кусочки бумаги. Если подобрать правильное сочетание материала и размера предмета, то в темноте наблюдаются небольшие искры, которые появляются вследствие разрядов электричества.

Электростатический фон часто появляется рядом с экраном телевизора при включении или выключении оборудования. Это поле ощущается в виде поднятых волосков на теле. Избыточный потенциал, полученный проводником извне, сосредотачивается на поверхности предмета, как становится ясно из проведенных опытов. Перемещение заряженных частиц к внешней оболочке свидетельствует о появлении электростатического поля внутри проводника, что дает импульс к переброске.

Существует ошибочное мнение, что электрический фон в заряженном теле исчезает после окончания дислокации электронов, а поле действует определенный промежуток времени. Если бы точка зрения была правильной, то избыточный потенциал мог находиться в условиях равновесия и способствовал бы беспорядочному и хаотичному движению молекул. Такое явление никогда не наблюдается в проводниках и заряженных телах.