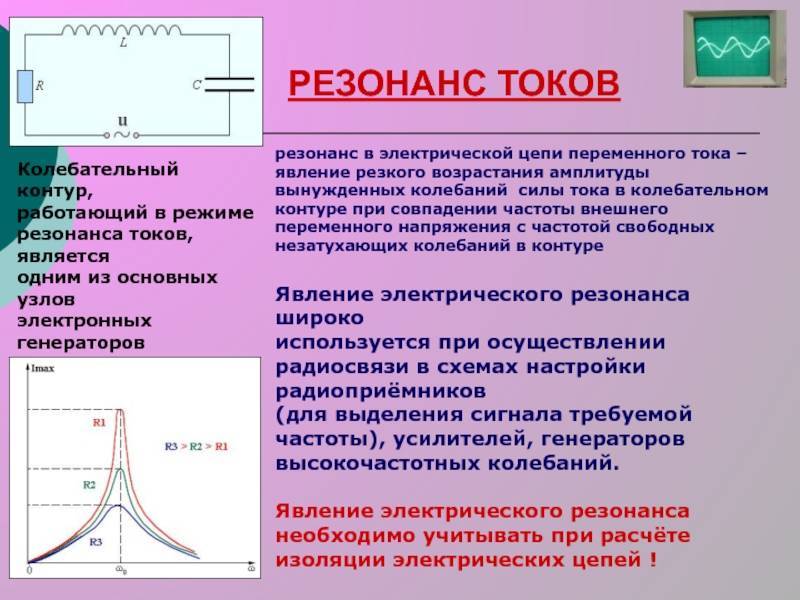
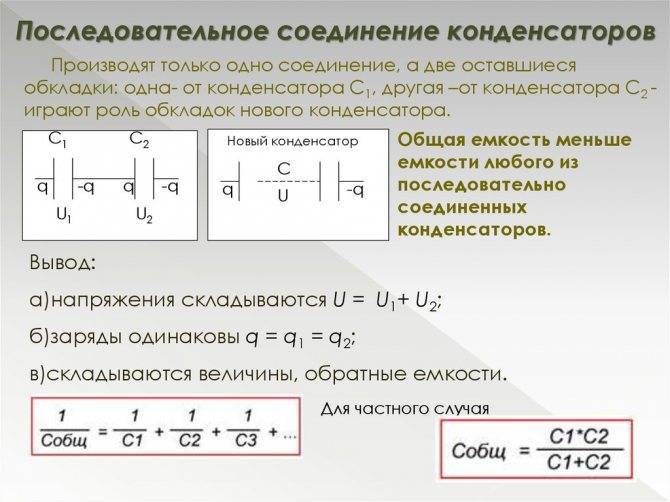
Резонанс в электрической цепи: причины резонанса

Содержание

Резонанс напряжения

Это явление возникнет, когда к генератору последовательно подключить катушку с конденсатором с одинаковыми реактивными сопротивлениями.

Обращаем ваше внимание, что ситуации, когда реактивными бывают только ёмкость и индуктивность, существуют только в идеале. А в реальности всегда есть сопротивление проводов, хотя и незначительное

При резонансном эффекте конденсатор с дросселем обмениваются энергией. При запуске генератора, конденсатор начинает накапливать энергию, а затем, после выключения, в результате обмена начинают происходить колебания.

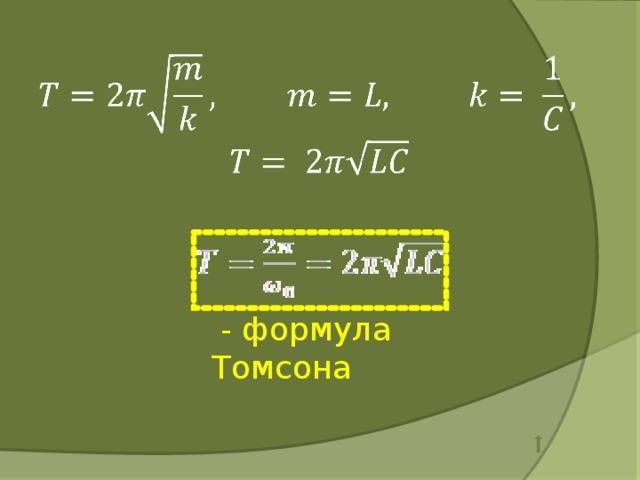
Периодичность вычисляется формулой Томпсона:

Поскольку сопротивление зависимо от частоты, соответственно, при увеличении частоты сопротивляемость индуктивности возрастает, при этом у ёмкости, наоборот, снижается.

Общий показатель сопротивления будет ощутимо понижаться, когда сопротивления одинаковые.

К главным показателям контура относятся частота и передаточный коэффициент. Если разобрать контур с четырьмя полюсами, становится понятно, что передаточный коэффициент равен добротности (Q).

В резонансе, чем значительнейпоказатель добротности, тем значительней напряжение на контурных элементах по сравнению с напряжением на генераторе.

В контуре показатели мощности падают из-за сопротивления. Энергия поставщика используется лишь для поддержки колебаний.

Виды и примеры резонанса

Только в самой физике различают такие виды резонанса как:

Механический резонанс – это все те же вышеупомянутые качели, резонанс моста от проходящей роты солдат, резонанс колокольного звона и т. д. Одним словом, резонанс, вызванный механическими воздействиями.
Акустический резонанс – это резонанс, благодаря которому работают все струнные музыкальные инструменты: гитара, скрипка, лютня, балалайка, банджо и т. д. К слову корпус музыкальных инструментов неспроста имеет свою форму. Звук, издаваемый струной при щипке, попадает внутрь корпуса и там вступает в резонанс со стенками, что в результате приводит к его усилению. По этой причине качество звучания той же гитары сильно зависит от того материала, из которого она сделана и даже от лака которым она покрыта.
Электрический резонанс – представляет собой совпадение частоты колебаний внешнего напряжения с частотой колебаний электрической цепи, по которой идет ток.

Помимо этих чисто физических резонансов есть еще уже упомянутый нами общественный резонанс – яркий отклик общества на какое-то событие (обычно политическое или экономическое), например брекзит Британии, ее выход из Европейского союза вызвал широкий общественный резонанс во многих странах Европы и особенно, разумеется, в самой Британии.

Есть также и когнитивный резонанс – это полное совпадение во взглядах и мнениях. Например, вы познакомились с новым человеком, а он думает так же как вы, у вас абсолютно схожие взгляды, вкусы, предпочтения, тогда имеет место когнитивный резонанс. И противоположное явление – когнитивный диссонанс, когда вы абсолютно не согласны с кем-то или чем-то, абсолютно не принимаете происходящего. (Например, автор этой статьи, оказавшись в каком-нибудь украинском бюрократическом учреждении, будь-то Жеке, БТИ или налоговой испытывает настоящий когнитивный диссонанс)).

2.11. Параллельный колебательной контур. Резонанс токов

Лекция 8

Рассмотрим параллельный колебательный контур, простейшим видом которого является параллельное соединение индуктивной катушки и конденсатора (рис. 2.17, а).

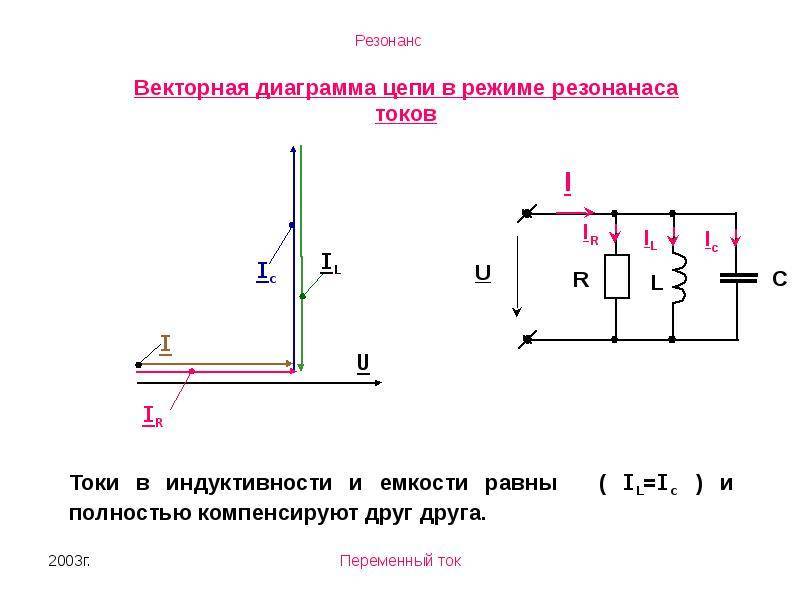
Резонансом токов называют такой режим параллельного колебательного контура, при котором ток в неразветвленной части цепи совпадает по фазе с напряжением а мощность, потребляемая из сети, равна активной мощности контура. Реактивная мощность при резонансе из сети не потребляется. Векторная диаграмма цепи при резонансе токов, представленная на рис. 2.17,6, выполнена согласно уравнению

Комплекс эквивалентной полной проводимости параллельного колебательного контура

Так как при резонансе угол сдвига фаз между током I0 и напряжением U равен нулю, т. е. то при резонансеилиСледовательно, ток при резонансе токов

(2.77)

Таким образом, резонанс токов наступает в цепи при взаимной компенсации токов реактивных проводимостей т. е. при взаимной компенсации индуктивной и реактивной емкостной проводимостей.

При резонансе токов эквивалентная полная проводимость контура Y

минимальная т. е. входное сопротивлениедостигает максимума, вследствие чего ток, идущий от сети, при резонансе токов будет минимален и равен

При резонансе токов и, следовательно, равны между собой реактивные токикоторые находятся в этом случае в противофазе. При резонансе токов возможны ситуации, когда реактивные токинамного превышают суммарный ток в цепи, вследствие чего резонанс при параллельном соединении называютрезонансом токов

. Это возможно при условии или

Отношение индуктивного или емкостноготоков при резонансе токов к суммарному токуназывается добротностью параллельного колебательного контура:

(2.78)

Затухание в параллельном контуре, как и в последовательном контуре, есть величина, обратная добротности:

Выразивчерез параметры цепи и частоту, определим резонансную частоту контура:

откуда найдем значение для резонансной угловой частоты:

(2.79)

В идеальном случае, например в радиотехнических устройствах, где применяют контуры с малыми потерями, когда практически (или они очень малы по сравнению с ρ), резонансную частотуможно определить, как и при резонансе в последовательном контуре, по формуле

Из формулы (2.79) видно, что резонанс токов возможен в цепи, если сопротивления r1 и r2 оба больше или оба меньше ρ

, ибо при невыполнении этого условия частотаокажется мнимой и, следовательно, в этом случае не существует частоты, при которой был бы резонанс. Прирезонансная частотарезонанс токов может наблюдаться при любой частоте, так как в этом случае эквивалентное сопротивление становится активным, не зависящим от частоты.

Так как при резонансе токов а значитто активная мощность Р равна полной мощности цепи, т. е.Реактивная мощностьQ

при резонансе токов равна нулю:

так как

Таким образом, при резонансе токов цепь не потребляет из сети реактивной энергии. Энергетические процессы, наблюдаемые в параллельном колебательном контуре, в этом случае аналогичны процессам, которые протекают при резонансе напряжений. В колебательном контуре происходит непрерывный взаимный обмен энергиями между емкостным и индуктивным элементами цепи, а сеть лишь компенсирует энергию, теряемую в активных сопротивлениях контура. Если бы параллельный колебательный контур состоял только из L и С, то его входное сопротивление при резонансе токов было бы бесконечно большим и ток из сети не поступал бы в контур, т. е. в этом случае энергия, сообщенная контуру при включении, не расходовалась бы, а периодически перекачивалась от магнитного к электрическому полю (и обратно), т. е. между индуктивным и емкостным элементами цепи, причем эти колебания продолжались бы неограниченное время.

Амплитуда резонанса

В КК при подаче переменного напряжения от внешнего источника наблюдаются два вида резонанса и резкое увеличение двух видов амплитуды: амплитуды тока и амплитуды напряжения.

Амплитуда тока

Амплитуда тока резко возрастает при резонансе напряжений в последовательном контуре (последовательный резонанс). Источник переменной ЭДС включён в цепь, где нагрузкой служат последовательно включённые элементы L и С.

В этом случае в цепь входят сопротивления: активное r и реактивное x, равное:

x = xL – xC.

Так как для внутренних колебаний xL и xC равны, то для тока, поступающего от генератора, при резонансе (когда частоты совпадают) эти значения тоже одинаковы. Поэтому x = 0. В итоге полное сопротивление цепи будет состоять только из небольшого активного сопротивления. Ток при этом получается максимальным.

Схема (а) и резонансные кривые (б) для резонанса напряжений

Амплитуда напряжения

Резонанс токов (параллельный резонанс) является условием резкого возрастания амплитуды напряжения. Источник ЭДС подключается вне контура и нагружен параллельно соединёнными элементами L и С. В этом случае на эффект резонанса влияет внутреннее сопротивление генератора. Амплитуда напряжения на контуре максимальна при малом отличии напряжения контура от напряжения генератора. Это возможно при малом Ri.

Внимание! Изменение частоты генератора меняет ток, а амплитуда напряжения на контуре не отстаёт по величине от напряжения на генераторе. Если, U = Е – I*Ri, где Е – ЭДС, I – ток, то при малом Ri U = Е. Схема (а) и резонансные кривые (б) для резонанса токов

Схема (а) и резонансные кривые (б) для резонанса токов

Формула для определения расчётной резонансной частоты для разных колебательных систем различается по входящим в неё параметрам. Несмотря на все различия, суть остаётся неизменной: эффект резонанса наступает тогда, когда частота внутренних колебаний системы и внешних воздействий становятся равны друг другу.

Область применения

Это явление в цепи колебательного контура имеет тенденцию к затуханию. Чтобы стало возможным использовать это явление в различных приборах и устройствах, необходимо постоянно поддерживать характеристики электричества в заданных пределах. Сделать этот процесс постоянным очень просто: достаточно подпитывать систему переменным напряжением с постоянными значениями частоты.

Радиовышка

Важно! Эффект резонанса широко применяется в различных радиопередающих и принимающих сигнал устройствах. Наиболее часто, это явление используется в различных фильтрах

Например, если на пути входящего электрического сигнала необходимо избавиться от составляющей определённой частоты, то параллельно проводнику устанавливают конденсатор, резистор и дроссель. Если фильтр необходим для того, чтобы «пропустить» сигнал определенной частоты, то также изготавливается фильтр из ёмкости, сопротивления и индуктивности, но подключается такая система последовательно

Наиболее часто, это явление используется в различных фильтрах. Например, если на пути входящего электрического сигнала необходимо избавиться от составляющей определённой частоты, то параллельно проводнику устанавливают конденсатор, резистор и дроссель. Если фильтр необходим для того, чтобы «пропустить» сигнал определенной частоты, то также изготавливается фильтр из ёмкости, сопротивления и индуктивности, но подключается такая система последовательно.

Электрический фильтр

Использовать эффект резонанса можно и для повышения напряжения. Например, в ситуации, когда электрический двигатель не способен работать на расчетных показателях мощности по причине низкого напряжения, достаточно установить по мощному конденсатору на каждую фазу, чтобы полностью разрешить проблему.

Резонанс в электрической цепи может возникать при наличии определенных условий, поэтому от него можно избавиться либо вызвать намеренно. Если такое явление является нежелательным, то, во многих случаях, достаточно изменить рабочую частоту или увеличить сопротивление, чтобы полностью устранить это паразитическое явление. Простейшая система этого типа состоит из конденсатора, резистора и дросселя, поэтому, при необходимости, можно легко собрать устройство, в котором это электрический эффект будет выполнять какую-либо полезную функцию.

Вам это будет интересно Особенности источников тока

Понятие о резонанс токов. Условия его возникновения и способы осуществления

Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.

Условие резонанса токов: , .

В1 – реактивная проводимость первой ветви,

В2 – реактивная проводимость второй ветви.

Способ возбуждения колебаний в электрическом контуре, заключающийся в генерации колебаний, за счет регулирования сигнала, управляющего возбуждением колебаний.

Резонанс токов и его признаки

Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.

Признаки резонанса токов:

Реактивные составляющие токов ветвей равны IPC = IPL и находятся в противофазе в случае, когда напряжение на входе чисто активное;

Токи ветвей превышают общий ток цепи, который имеет минимальное значение и совпадают по фазе.

Мгновенная мощь цепи синусоидального тока

Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.

Пусть мгновенные напряжение и ток определяются по формулам:

Среднее значение мгновенной мощности за период

Из треугольника сопротивлений , a

Получим еще одну формулу:

Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P.

Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.

Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе , так как напряжение и ток в индуктивности или емкости различаются по фазе на 90 o . В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов.

Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.

Преобразуем выражение (6.23):

где — мгновенная мощность в активном сопротивлении;

— мгновенная мощность в реактивном элементе (в индуктивности или в емкости).

Максимальное или амплитудное значение мощности p2 называется реактивной мощностью

где x — реактивное сопротивление (индуктивное или емкостное).

Реактивная мощность, измеряемая в вольтамперах реактивных, расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.

Причины резонанса

Классический пример с приказом командира идти марширующим солдатам «не в ногу» перед мостом наглядно демонстрирует суть этого явления

Если не использовать такую предосторожность, колебания могут увеличиться до критичного значения, вплоть до разрушения конструкции. Для получения максимальной амплитуды раскачивают в определенном ритме качели. Приведенные примеры демонстрируют существенное увеличение результата при совпадении частот внешнего воздействия и непосредственно самой системы

Приведенные примеры демонстрируют существенное увеличение результата при совпадении частот внешнего воздействия и непосредственно самой системы.

Электрический резонанс по своим принципам не отличается от механических аналогов. Он образуется при совпадении частот внешнего сигнала и контура. Функции накопителей энергии выполняют реактивные индукционные и емкостные элементы. Потери (постепенное уменьшение амплитуды) обеспечивает электрическое сопротивление цепи, что аналогично коэффициенту трения.

Резонанс токов в цепи с переменным током

Протекание тока внутри электрической цепи с последовательным, параллельным или смешанным типом соединения элементов, вызывает получение различных режимов функционирования.

Таким образом, резонанс электрической цепи является режимом участка, который содержит элементы индуктивного и емкостного типа, а угол фазового сдвига между токовыми величинами и показателями напряжения нулевые.

В соединяемых параллельным способом конденсаторе и катушечной части наблюдается равное реактивное сопротивление, чем обусловлен резонанс.

Также должен учитываться тот факт, что для катушечной части и конденсатора характерно полное отсутствие активного сопротивления, а равенство реактивного сопротивления делает нулевыми общие токовые показатели внутри неразветвленной части электрической цепи и большие величины тока в ветвях.

В условиях параллельного соединения индуктивной катушки и конденсатора получается колебательный контур, который отличается наличием создающего колебания генератора, не подключенного в контур, что делает систему замкнутой.

Явление, сопровождающееся резким уменьшением амплитуды силы токовых величин внешней цепи, которая используется для питания параллельно включенного конденсатора и обычной индуктивной катушки в условиях приближения частоты приложенного напряжения к частоте резонанса, носит название токового или параллельного резонанса.

Что такое резонанс

Явление резонанса впервые было описано Галилео Галилеем в 1602 году в работах, посвящённых исследованию маятников и музыкальных струн. В этой области итальянский физик сделал много открытий, которые послужили основой для дальнейшего изучения феномена.Резонанс в физике — это частотно-избирательный отклик колебательной системы на периодическое воздействие извне, проявляющееся в синхронизации частот колебаний системы с частотой внешнего воздействия, что влечет за собой резкое увеличение амплитуды колебаний этой системы.

Иначе говоря, резонанс — это отклик на некий внешний раздражитель. Представьте, что на тело, находящееся в состоянии покоя или совершающее амплитудные движения определенной частоты, начал оказывать воздействие раздражитель извне с собственной амплитудой и частотой. Если эта внешняя сила просто выведет тело из равновесия, а затем перестанет действовать, то оно какое-то время станет колебаться около своего положения равновесия. Частота этих колебаний является собственной частотой колебаний тела. Если же движение внешнего раздражителя, выводящего тело из равновесия, совпадет с его частотой, то амплитуда тела станет увеличиваться.

Чтобы упростить понимание явления, для примера обычно приводят механизм катания на качелях. Если после раскачивания, сидя на качелях, не вмешиваться в процесс, то через пару минут они остановятся.Но если во время «полета» подталкивать их своим телом по направлению движения, амплитуда будет возрастать, и качели продолжат совершать вынужденные колебания.

Колебания — процесс изменения состояний системы, которые повторяются через определенные промежутки времени.

По отношению к качелям ваши движения являются внешней силой, которая вынуждает их подниматься выше. Причем сила воздействия не так важна. Даже небольшое движение внешней силы при совпадении с частотой системы, может увеличить ее амплитуду. Так, маленькому ребенку удается раскачать взрослого человека, подстроившись под движение качелей.

Частота колебаний измеряется в герцах (1 Гц) и обозначает количество колебаний в секунду. Например, частота колебаний в 20 Гц говорит о том, что тело совершает 20 колебаний в одну секунду.

Резонировать могут любые упругие физические тела — твердые, жидкие, газообразные. Главным условием резонанса является наличие у тела собственной резонансной частоты.

Механические колебания маятника

Самая простая модель, которая может наглядно показать колебания, это простейший маятник, а точнее математический маятник. Колебания разделяют на свободные и вынужденные. Первоначально воздействующая энергия на маятник обеспечивает в теле свободные колебания без присутствия внешнего источника переменной энергии воздействия. Данная энергия может быть как кинетической, так и потенциальной.

Здесь не имеет значение насколько сильно или нет качается сам маятник, — время, потраченное на прохождения его пути в прямом и обратном направлении, сохраняется неизменным. Во избежание недоразумений с затуханием колебаний вследствие трения о воздух стоит выделить, что для свободных колебаний должны соблюдаться условия возврата маятника в точку равновесия и отсутствия трения.

А вот частота в свою очередь напрямую зависит от величины длины нити маятника. Чем короче нить, тем выше частота и наоборот.

Возникающая естественная частота тела под воздействием первоначально приложенной силы называется резонансной частотой.

Все тела, которым свойственны колебания, совершают их с заданной частотой. Для поддержания в теле незатухающих колебаний необходимо обеспечить постоянную периодическую энергетическую «подпитку». Это достигается воздействием в одновременный такт колебаний тела постоянной силы с определенным периодом. Таким образом возникающие колебания в теле под действием периодической силы снаружи называют вынужденными.

В какой-то момент внешних воздействий возникает резкий скачок амплитуды. Такой эффект возникает если периоды внутренних колебаний тела совпадают с периодами внешней силы и называется резонансом. Для возникновения резонанса достаточно совсем небольших величин внешних источников воздействия, но с обязательным условием повторения в такт. Естественно, при фактических расчетах в земных условиях не стоит забывать о действии сил трения и сопротивления воздуха на поверхность тело.

§56. Резонанс напряжений и резонанс токов

Явление резонанса.

Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими.

При подсоединении колебательного контура к источнику переменного тока угловая частота источника ω может оказаться равной угловой частоте ω, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ω, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ω, сообщаемых этой системе внешними силами.

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ω источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ω, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

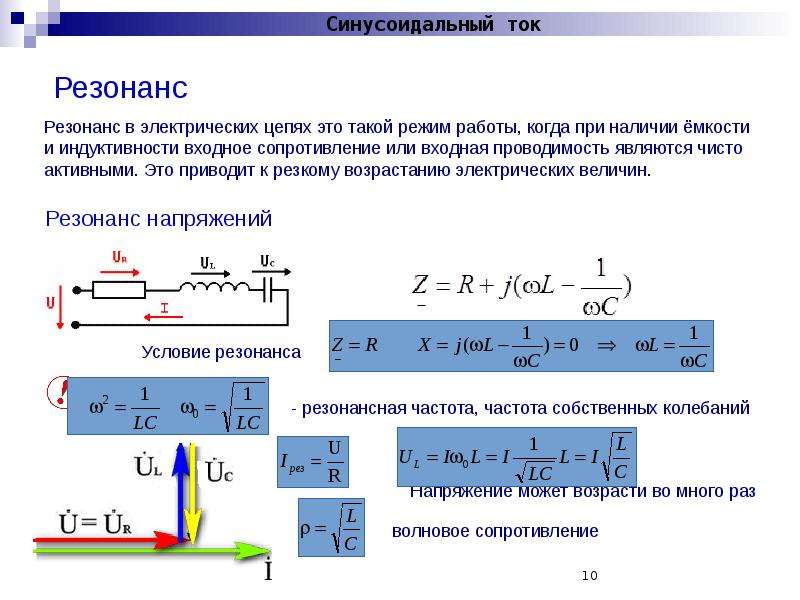
Резонанс напряжений.

При резонансе напряжений (рис. 196, а) индуктивное сопротивление XL равно емкостному Хси полное сопротивление Z становится равным активному сопротивлению R:

В этом случае напряжения на индуктивности UL и емкости Uc равны и находятся в противофазе (рис. 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = XL—Xс становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений UL и Uc, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.

Угловая частота ω0, при которой имеют место условия резонанса, определяется из равенства ωoL = 1/(ωС).

Рис. 196. Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений

Если плавно изменять угловую частоту ω источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при ωo), а затем увеличивается (рис. 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.

Рис. 197. Зависимость тока I и полного сопротивления Z от ω для последовательной (а) и параллельной (б) цепей переменного тока

Резонанс токов.

Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R1=R2 = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость, т. е. ωoL = 1/(ωoC).

Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов

Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части цепи при резонансе I=U √(G 2 +(BL-BC) 2 )= 0. Значения токов в ветвях I1 и I2 будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°).

Векторная диаграмма токов и напряжений

Для решения уравнения вынужденных колебаний мы можем использовать достаточно наглядный метод векторных диаграмм. Для этого используем векторную диаграмму, на которой с помощью векторов изобразим колебания определенной заданной частоты ω.

Давайте посмотрим, как построить векторную диаграмму токов и напряжений.

Рисунок 2.3.2. Векторная диаграмма, на которой с помощью векторов изображены гармонические колебания A cos(ωt+φ1), B cos(ωt+φ2) и их суммы C cos(ωt+φ).

Наклон векторов к горизонтальной оси определяется фазой колебаний φ1 и φ2, а длины векторов соответствуют амплитудам колебаний A и B. Относительный фазовый сдвиг определяет взаимную ориентацию векторов: ∆φ=φ1-φ2. Для того, чтобы построить вектор, изображающий суммарное колебание, нам необходимо использовать правило сложения векторов: C→=A→+B→.

При вынужденных колебаниях в электрической цепи для построения векторной диаграммы напряжений и токов нам необходимо знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для любого участка цепи.

Источник переменного тока может быть подключен к:

катушке индуктивности L;
резистору с сопротивлением R;
конденсатору с емкостью С.

Рассмотрим эти три примера подробнее. Будем считать, что напряжение на резисторе, катушке и конденсаторе во всех трех случаях равно напряжению внешнего источника переменного тока.

Резистор в цепи переменного тока

JRR=uR=URcos ωt; JR=URRcos ωt=IRcos ωt

Мы обозначили амплитуду тока, который протекает через резистор, через IR. Соотношение RIR=UR выражает связь между амплитудами тока и напряжения на резисторе. Фазовый сдвиг в этом случае равен нулю. Физическая величина R – это активное сопротивление на резисторе.

Конденсатор в цепи переменного тока

Запишем формулу:

uC=qC=UCcos ωt

JC=dqdt=CduCdt=CUC(-ωsin ωt)=ωCUCcosωt+π2=ICcosωt+π2.

Соотношение между амплитудами тока IC и напряжения UC: 1ωCIC=UC.

Ток опережает по фазе напряжение на угол π2.

Определение 4

Физическая величина XC=1ωC — это емкостное сопротивление конденсатора.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Катушка в цепи переменного тока

Запишем формулы:

UL=LdJLdt=ULcos ωt;JL=∫ULLcos ωt dt=ULωLsin ωt=ULωLcos ωt-π2=ILcosωt-π2

Соотношение между амплитудами тока IL и напряжения UL: ωLIL=UL.

Ток отстает по фазе от напряжения на угол π2.

Определение 5

Физическая величина XL=ωL — это индуктивное сопротивление катушки.

Построим векторную диаграмму для последовательного RLC-контура, частота вынужденных колебаний в котором ω.

При построении диаграммы будем учитывать, что через различные участки цепи протекает один и тот же ток. Удобнее делать это будет относительно вектора, который изображает колебания тока в цепи.

Для амплитуды тока введем обозначение I. Фазу тока примем равной нулю, так как в данном случае нас интересуют не столько абсолютные значения фаз, сколько относительные фазовые сдвиги.

Рисунок 2.3.3. Векторная диаграмма для последовательной RLC-цепи.

Данная диаграмма построена для случая, когда ωL>1ωC или ω2>ω2=1LC.

По фазе напряжение внешнего источника опережает ток, который течет в цепи, на некоторый угол φ.

Из рисунка видно, что

ε2=UR2+(UL-UC)2, откуда следует, что

I=εR2+ωL-1ωC2; tg φ=ωL-1ωCR.

Из выражения для I видно, что амплитуда тока принимает максимальное значение при условии

ωL-1ωC= или ω2=ωрез2=ω2=1LC.

Заключение

Резонанс напряжений и токов — интересное явление, о котором нужно знать. Он наблюдается только в индуктивно-емкостных цепях. В цепях с большим активным сопротивлениям он не может возникнуть. Подведем итоги, кратко ответив на основные вопросы по этой теме:

Где и в каких цепях наблюдается явление резонанса?

В индуктивно-емкостных цепях.

Какие условия возникновения резонанса токов и напряжений?

Возникает при условии равенства реактивных сопротивлений. В цепи должно быть минимальное активное сопротивление, а частота источника питания совпадать с резонансной частотой контура.

Как найти резонансную частоту?

В обоих случаях по формуле: w=(1/LC)^(1/2)

Как устранить явление?

Увеличив активное сопротивление в цепи или изменив частоту.

Теперь вы знаете, что такое резонанс токов и напряжений, каковы условия его возникновения и варианты применения на практике. Для закрепления материала рекомендуем просмотреть полезное видео по теме:

Материалы по теме: