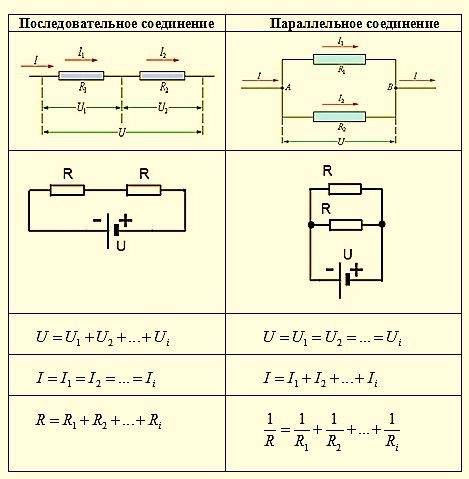
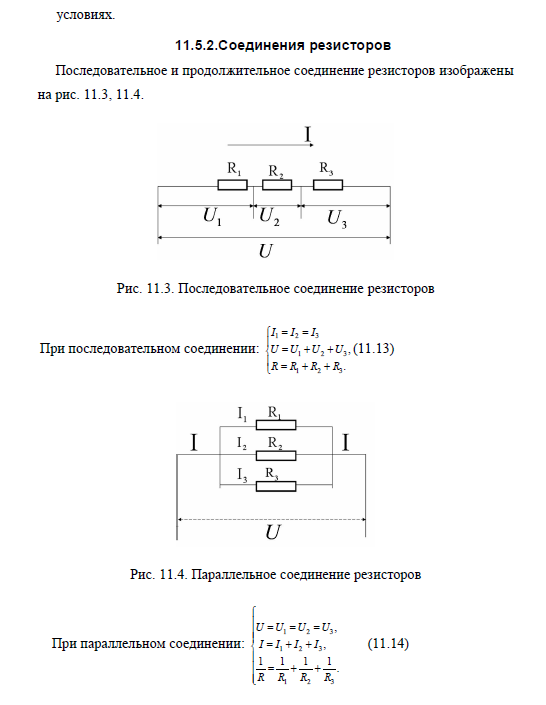
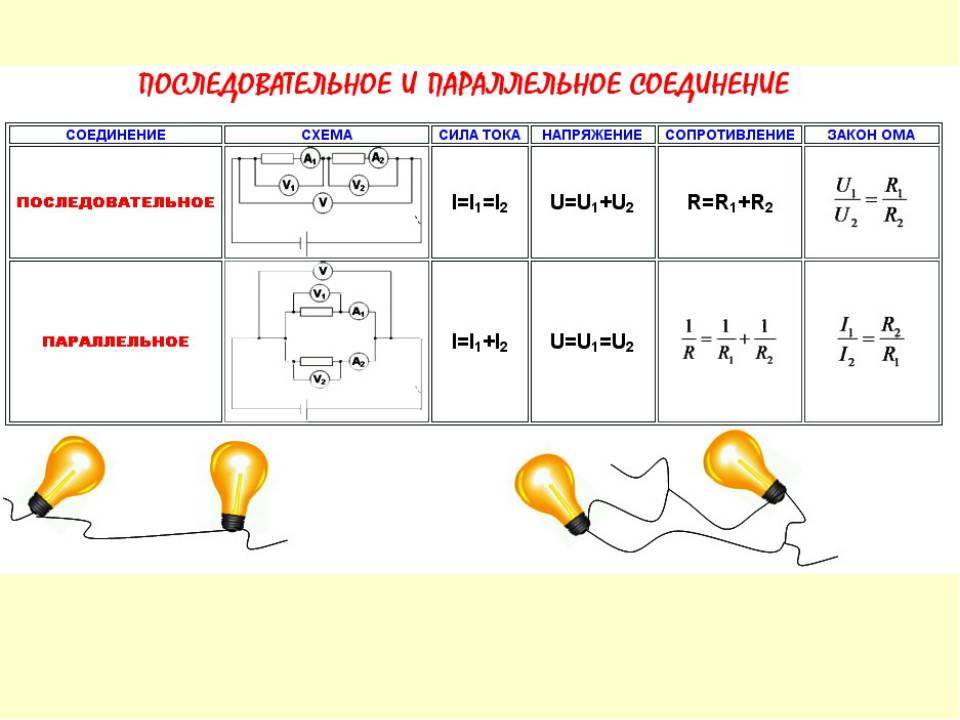
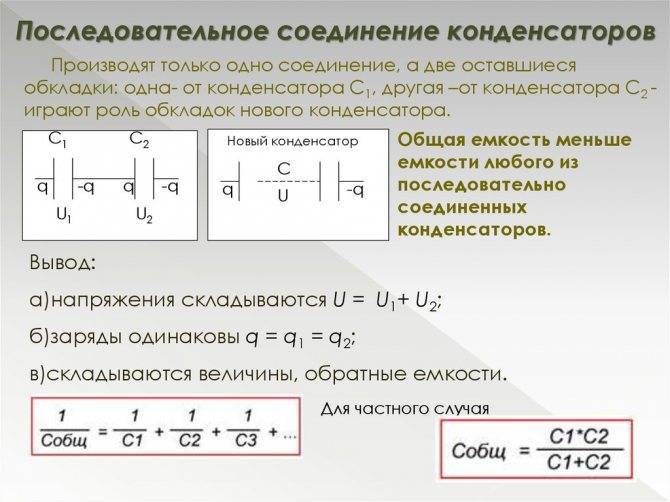
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
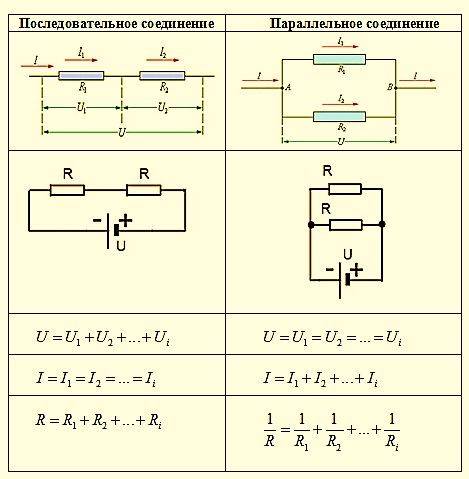
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Что такое параллельное соединение проводников
При данном способе в составе схемы в крайних точках соединяются начала и концы всех нагрузок, подключенных к источнику электротока. Сами же нагрузки размещаются параллельно по отношению друг к другу. Количество подключенных по такой схеме компонентов не ограничивается. Схема используется во многих сферах, позволяя решать разные задачи компоновки сетей. Например, часто задействуют параллельное соединение аккумуляторов.
При контрольном измерении значения вольтажа электроприборов вольтметр будет показывать одинаковые величины. Это означает, что электронапряжение на каждой нагрузке будет равняться общей величине вольтажа, действующего в электрической цепи.
Особенностью схемы параллельного соединения можно назвать разветвление цепи. В месте разветвления происходит деление заряда с направлением его частей по отдельной линии к соответствующему проводнику. Поэтому общая величина тока будет равна суммарному значению токов на каждой из включенных нагрузок.
Совокупное электрическое сопротивление всей электроцепи имеет меньшее абсолютное значение, по сравнению с каждым из приборов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное. На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения – параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Упражнения
Упражнение №1
Цепь состоит из двух последовательно соединённых проводников, сопротивление которых $4 \space Ом$ и $6 \space Ом$. Сила тока в цепи равна $0.2 \space А$. Найдите напряжение на каждом из проводников и общее напряжение.
Дано:$R_1 = 4 \space Ом$$R_2 = 6 \space Ом$
$I = 0.2 \space А$
$U_1 — ?$$U_2 — ?$$U — ?$
Показать решение и ответ
Скрыть
Решение:
Используя закон Ома для участка цепи, мы рассчитаем значения напряжения на концах первого и второго проводников. Сила тока на всех участках цепи одинакова.
Напряжение на концах первого проводника:$I = \frac{U_1}{R_1}$,$U_1 = IR_1$,$U_1 = 0.2 \space А \cdot 4 \space Ом = 0.8 \space В$.
Напряжение на концах второго проводника:$I = \frac{U_2}{R_2}$,$U_2 = IR_2$,$U_2 = 0.2 \space А \cdot 6 \space Ом = 1.2 \space В$.
Общее напряжение будет равно сумме напряжений на концах каждого проводника:$U = U_1 + U_2$,$U = 0.8 \space В + 1.2 \space В = 2 \space В$.
Ответ: $U_1 = 0.8 \space В$, $U_2 = 1.2 \space В$, $U = 2 \space В$.
Упражнение №2
Для электропоездов применяют напряжение, равное $3000 \space В$. Как можно использовать для освещения вагонов лампы, рассчитанные на напряжение $50 \space В$ каждая?
Такие лампы можно соединить последовательно в одну цепь. Главное, чтобы их суммарное напряжение не превышало общее. Рассчитаем количество таких ламп, которое мы можем включить в цепь.
Дано:$U = 3000 \space В$$U_1 = 50 \space В$
$n — ?$
Показать решение и ответ
Скрыть
Решение:
Все лампы будут иметь одинаковое напряжение в $50 \space В$. Напряжение на всей цепи равно сумме напряжений на каждой лампе. Тогда:$n = \frac{U}{U_1}$,$n = \frac{3000 \space В}{50 \space} = 60$.
Получается, что в таком электропоезде мы можем разместить 60 ламп для освещения вагонов, соединив их последовательно.
Ответ: при последовательном соединении мы можем использовать $n = 60$ ламп.
Упражнение №3
Две одинаковые лампы, рассчитанные на $220 \space В$ каждая, соединены последовательно и включены в сеть с напряжением $220 \space В$. Под каким напряжением будет находиться каждая лампа?
Дано:
$U = 220 \space В$
$U_1 — ?$$U_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Лампы соединены последовательно. Значит, $U = U_1 + U_2$.
Если лампы одинаковые, то они имеют одинаковые сопротивления $R$. Сила тока тоже одинакова в каждой лампе. Из этого мы можем сделать вывод, что напряжение на лампах будет одинаковым:$U_1 = IR$, $U_2 = IR$, $U_1 = U_2$.
Тогда мы можем записать следующее:$U = U_1 + U_2 = 2U_1$.
Рассчитаем напряжение на одной лампе:$U_1 = U_2 = \frac{U}{2}$,
$U_1 = U_2 = \frac{220 \space В}{2} = 110 \space В$.
Ответ: $U_1 = U_2 = 110 \space В$.
Упражнение №4
Электрическая цепь состоит из источника тока — батареи аккумуляторов, создающей в цепи напряжение, равное $6 \space В$, лампочки от карманного фонаря с сопротивлением в $13.5 \space Ом$, двух спиралей c сопротивлением $3 \space Ом$ и $2 \space Ом$, ключа и соединительных проводов. Все детали цепи соединены последовательно. Начертите схему цепи. Определите силу тока в цепи, напряжение на концах каждого из потребителей тока.
Схема такой цепи изображена на рисунке 5.
Рисунок 5. Схема электрической цепи к упражнению №4
Дано:$U = 6 \space В$$R_1 = 13.5 \space Ом$$R_2 = 3 \space Ом$$R_3 = 2 \space Ом$
$I — ?$$U_1 — ?$$U_2 — ?$$U_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем общее сопротивление на всей цепи:$R = R_1 + R_2 + R_3$,$R = 13.5 \space Ом + 3 \space Ом + 2 \space Ом = 18.5 \space Ом$.
Теперь используем закон Ома для того, чтобы рассчитать силу тока в цепи:$I = \frac{U}{R}$,$I = \frac{6 \space В}{18.5 \space Ом} \approx 0.32 \space А$.
Сила тока на каждом участке цепи при последовательном соединении элементов будет одинакова. Теперь мы будем использовать закон Ома отдельно для каждого проводника.
Рассчитаем напряжение на лампочке от карманного фонаря:$U_1 = IR_1$,$U_1 = 0.32 \space А \cdot 13.5 \space Ом \approx 4.3 \space В$.
Рассчитаем напряжение на первой спирали:$U_2 = IR_2$,$U_2 = 0.32 \space А \cdot 3 \space Ом \approx 1 \space В$.
Рассчитаем напряжение на второй спирали:$U_3 = IR_3$,$U_3 = 0.32 \space А \cdot 2 \space Ом \approx 0.6 \space В$.
Ответ: $I \approx 0.32 \space А$, $U_1 \approx 4.3 \space В$, $U_2 \approx 1 \space В$, $U_3 \approx 0.6 \space В$.
Соединение резисторов — пример расчета
В качестве примера смешанного соединения резисторов рассмотрим систему распределения электроэнергии и систему заземления в частном доме. Несмотря на то, что данная схема отношения к электронике не имеет, а в качестве резисторов выступают контуры заземления, все же принципы одни и те же. К тому же, вместо того, чтобы рассматривать произвольную цепь, намного интересней и познавательней дополнительно разобраться в вопросах электричества в быту.
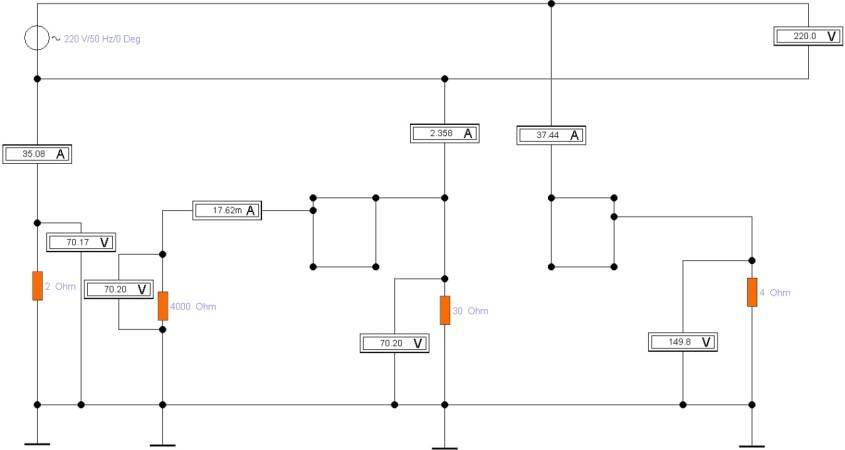
На приведенной выше схеме показана система распределения электроэнергии по системе TN-C-S. Слева направо:
- Источник питания U = 220 В (распределительный трансформатор) с глухозаземленной нейтралью R1 = 2 Ом.
- Далее R2 = 4000 Ом — это имитация прикосновения человека к зануленному корпусу, находящемуся в доме с системой заземления TN-C-S.
- R3 = 30 Ом — повторное заземление в доме с системой TN-C-S.
- R4 = 4 Ом — сопротивление контура заземления (система TT) в соседнем доме.
В доме с системой заземления TT смоделирован пробой фазы на корпус при неработающей автоматике отключения питания. Поэтому потенциал через землю направился к нейтрали трансформатора по трем путям (участок параллельного соединения):
- Через заземление 30 Ом соединенное с нейтралью (рабочий нулевой проводник).
- Через землю — пол — человека — зануленный прибор (4000 Ом).
- Через заземление нейтрали трансформатора 2 Ом.
Получаем параллельное соединение резисторов — R1, R2, R3, и последовательное соединение — R4 и группа с параллельным соединением.
Прежде чем переходить к расчету в цепи со смешанным соединением резисторов, отметим, о чем данная симуляция свидетельствует. Нельзя допускать в одной системе распределения электроэнергии наличия различных систем заземления. Так, согласно приведенной модели, при пробое фазы на корпус в системе TT произошел вынос опасного потенциала 70 В на корпус прибора в соседнем доме с системой заземления TN-C-S. Выносимый потенциал будет снижаться, если в цепи с параллельным соединением будет снижаться общее сопротивление.
Рассчитаем, на сколько снизится выносимый потенциал (напряжение), если добавить в участок с параллельным соединением еще 29 домов с системой заземления TN-C-S (сопротивление повторного заземления каждого дома 30 Ом).
Согласно методике расчета в первую очередь определим общее сопротивление на участке с параллельным соединением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + 1 / R4 = 1 / 2 + 1 / 4000 + 1 / 30 + 29 / 30 = 1,5 Ом.
R = 1 / 1,5 = 0,67 Ом.
Теперь можно рассмотреть последовательное соединение с резисторами R123(+29 по 30 Ом) = 0,67 Ом и R4 = 4 Ом. R = R123(+29 по 30 Ом) + R4 = 4,67. Зная напряжение, находим силу тока:
I = U / R = 220 / (4 ,67) = 47,1 A.
Зная силу тока, найдем напряжение на участке с параллельным соединением резисторов (где общее сопротивление 0,67 Ом):
U123(+29 по 30 Ом) = R123(+29 по 30 Ом) × I = 0,67 × 47,1 = 31,5 В.
Как видно с добавлением в участок с параллельным соединением 29 дополнительных резисторов с сопротивлением каждого 30 Ом общее сопротивление и напряжение снизились. И, несмотря на то, что ток всей цепи возрос, ток проходящий через человека (R2 = 4000 Ом) значительно снизился за счет снижения напряжения участка цепи. Если посмотреть схему, то изначально через тело человека проходило 17,6 mA. После добавления 29 резисторов это значение снизилось: I2 = U123(+29 по 30 Ом) / R2 = 31,5 / 4000 = 0,0078 A = 7,8 mA.
Подведем итог. При различном соединении резисторов расчет их общих сопротивлений выполняется в соответствии с простыми формулами. И помимо изменения сопротивления в цепи, согласно закону Ома можно проанализировать также такие параметры, как сила тока и напряжение на различных участках.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
Читать также: Разводка отопления медными трубами
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения – паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Как рассчитать мощность резистора?
Мощность рассеивания резистора
У резистора есть довольно важный параметр, который целиком и полностью влияет на надёжность его работы. Этот параметр называется мощностью рассеивания. Он уже упоминался в статье о параметрах резистора.
Сама по себе мощность постоянного тока рассчитывается по простой формуле:
Здесь, P(Вт) – мощность;
U(В) – напряжение;
(А)
Как видим, мощность зависит от напряжения и тока. В реальной цепи через резистор протекает определённый ток. Поскольку резистор обладает сопротивлением, то под действием протекающего тока резистор нагревается. На нём выделяется какое-то количество тепла. Это и есть та мощность, которая рассеивается на резисторе.
Если в схему установить резистор меньшей мощности рассеивания, чем требуется, то резистор будет нагреваться и в результате сгорит. Поэтому, если в схеме нужно заменить резистор мощностью 0,5 Ватт, то ставим на 0,5 Ватт и более. Но никак не меньше!
Каждый резистор рассчитан на свою мощность. Стандартный ряд мощностей рассеивания резисторов состоит из значений:
- 0,125 Вт
- 0,25 Вт
- 0,5 Вт
- 1 Вт
- 2 Вт
- Более 2 Вт.
Чем больше резистор по размерам, тем, как правило, на большую мощность рассеивания он рассчитан.
Допустим, у нас есть резистор с номинальным сопротивлением 100 Ом. Через него течёт ток 0,1 Ампер. На какую мощность должен быть рассчитан этот резистор?
Тут нам потребуется формула. Выглядит она так:
Здесь, P(Вт) – мощность;
R(Ом) – сопротивление цепи (в данном случае резистора);
I(А) – ток, протекающий через резистор.
Все расчёты следует производить, строго соблюдая размерность. Так, если сопротивление резистора не 100 Ом, а 1 кОм, то в формулу нужно подставить значение в Омах, т.е. 1000 Ом (1 кОм = 1000 Ом). Тоже правило касается и других величин (тока, напряжения).
Рассчитаем мощность для нашего резистора:
Мы получили мощность 1 Ватт. Теперь небольшое отступление.
В реальную схему необходимо устанавливать резистор с мощностью в полтора – два раза выше рассчитанной.
Поэтому нам подойдёт резистор мощностью 2 Вт (см. резисторов).
Также есть и другая формула для расчёта мощности. Она применяется в том случае, если неизвестен ток, который протекает через резистор.
Всё бы хорошо, но в жизни бывают случаи, когда применяется последовательное или параллельное соединение резисторов. Как рассчитать мощность рассеивания для каждого из резисторов в последовательной или параллельной цепи?
Допустим, нам требуется заменить резистор сопротивлением 100 Ом. Протекающий через него ток равен 0,1 Ампер. Следовательно, мощность этого резистора 1 Ватт.
Для его замены можно применить два соединённых последовательно резистора сопротивлением 20 Ом и 80 Ом. На какую мощность должны быть рассчитаны эти резисторы?
Для последовательной цепи действует одно правило. Через последовательно соединённые резисторы течёт один и тот же ток. Теперь применим формулу для расчёта мощности и получим, что мощность рассеивания резистора на 20 Ом должна быть равна 0,2 Вт, а резистора на 80 Ом — 0,8 Вт. Выбираем резисторы согласно стандартному ряду мощностей:
R1 – 20 Ом (0,5 Вт);
R2 – 80 Ом (1 Вт)
Как видим, если сопротивления резисторов будут разные, то и мощность на них будет выделяться разная.
Мощность, рассеивающаяся на резисторе, зависит в первую очередь от тока, который течёт через данный резистор. А ток зависит от сопротивления резистора. Поэтому, если вы соединяете последовательно резисторы разных номиналов, то и рассеивающаяся мощность распределиться между ними.
Это обстоятельство необходимо учитывать при самостоятельном конструировании электронных самоделок иначе при неправильном подборе резисторов может получиться так, что на одном резисторе выделиться больше мощности, чем на другом, и он будет работать в тяжёлом температурном режиме.
Чтобы не ломать голову и не рассчитывать мощность каждого в отдельности резистора, можно поступать так:
Мощность каждого резистора, входящего в составляемую нами цепь (параллельную или последовательную) должна быть равна мощности заменяемого резистора. Иными словами, если нам надо заменить резистор, мощностью 1 Вт, то каждый из резисторов для его замены должен иметь мощность не менее 1 Ватта. На практике это самое быстрое и эффективное решение.
Для параллельного соединения резисторов нужно учитывать, что через резистор с меньшим сопротивлением протекает больший ток. Следовательно, и мощности на нём будет рассеиваться больше.
Нравится
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях, будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
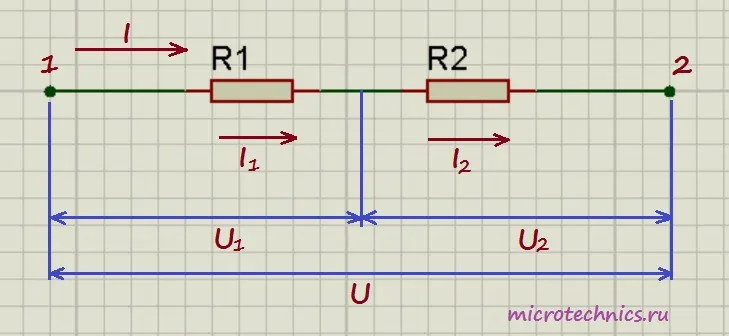
Здесь у нас классический случай последовательного соединения — два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
I = I_1 = I_2
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
U = U_1 + U_2
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
U_1 = I_1R_1 = IR_1
U_2 = I_2R_2 = IR_2
Тогда для вычисления общего напряжения можно использовать следующее выражение:
U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)
Но для общего напряжения также справедлив закон Ома:
U = IR_0
Здесь R_0 — это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
R_0 = R_1 + R_2
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например, для следующей цепи:
Общее сопротивление будет равно:
R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление, будет работать в любом случае. А если при последовательном соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:
R_0 = nR
В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Расчет мощности при последовательном соединении

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом. Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны. Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
Основные параметры последовательного и параллельного подключений
Типы подключений следует различать из-за особенностей
основных параметров электрической цепи при таких подключениях.
При параллельном подключении, напряжение на элементах цепи всегда будет постоянным, а сила тока суммируется из токов на каждом элементе. Есть еще такой параметр, как сопротивление. Мы не рекомендуем заучивать наизусть все формулы, а руководствоваться законом Ома, предположив, что один из параметров будет постоянным. Но для ускорения решения задач заучить выкладку может быть полезно. Собственно, там отношение единицы к сопротивлению цепи, равно сумме отношений 1 к каждому из сопротивлений.
При последовательном подключении, напряжение на каждом элементе будет суммироваться, а сила тока будет постоянной. Сопротивление мы также можем узнать из закона Ома. Или же запомнить, что сопротивление равно сумме сопротивлений элементов цепи.
Особенности параметров при последовательном и параллельном подключениях можно легко запомнить, если представить, что соединительные провода – это трубы, а электрический ток вода. Сравнить с водой тут можно именно силу тока. Почему же силу тока? Потому что ток характеризуется количеством заряженных частиц (читай, как наличие воды в трубе).
Представим, что в случае последовательного подключения мы соединяем две трубы одинакового сечения (представим именно одинаковое сечение, т.к. дальше уже начинают влиять такие параметры, как сопротивление) и в каждой трубе есть вода при её наличии в водопроводе. Если же мы соединим две трубы параллельно, то поток распределится равномерно (а на деле в соответствии с геометрическими параметрами труб) между двумя трубами, т.е сила тока будет суммироваться из всех участков.
Почему всё происходит именно так и почему при параллельном подключении ток распределяется именно по двум проводникам и суммируется? Это сложный фундаментальный вопрос, обсуждение которого займет ни одну статью. На данный момент предлагаю считать, что это просто свойство, которое нужно знать. Как и то, что лёд ощущается холодным, а огонь горячим.
При смешанном
подключении мы предварительно должны разбить цепь на простые для понимания
участки, а затем проанализировать, как они в итоге будут соединены.
Соответственно, на выходе мы получим простой вариант несложного подключения,
которое однозначно будет или последовательное, или параллельное.
Зная все эти параметры, мы легко можем проанализировать любую электрическую цепь и собрать новую с нужными параметрами.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением \( R_1 \) и \( R_2 \). Напряжения на резисторах соответственно \( U_1 \) и \( U_2 \).
По какой из формул можно определить напряжение U на участке АВ?
1) \( U=U_1+U_2 \)
2) \( U=U_1-U_2 \)
3) \( U=U_1=U_2 \)
4) \( U=\frac{U_1U_2}{U_1+U_2} \)
2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением \( R_1 \) и \( R_2 \). Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) \( I=I_1=I_2 \)
2) \( I=I_1+I_2 \)
3) \( U=U_1+U_2 \)
4) \( R=R_1+R_2 \)
3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R} и R2. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) \( U=U_1+U_2 \)
2) \( I=I_1+I_2 \)
3) \( U=U_1=U_2 \)
4) \( R=\frac{R_1R_2}{R_1+R_2} \)
4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением \( R_1 \) и \( R_2 \). Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) \( U=U_1=U_2 \)
2) \( I=I_1+I_2 \)
3) \( I=I_1=I_2 \)
4) \( R=\frac{R_1R_2}{R_1+R_2} \)
5. На рисунке изображена схема электрической цепи. В эту цепь параллельно включены два одинаковых резистора сопротивлением \( R_1 \). По какой из формул можно определить общее сопротивление цепи \( R \)?
1) \( R=R_1{}^2 \)
2) \( R=2R_1 \)
3) \( R=\frac{R_1}{2} \)
4) \( R=\sqrt{R_1} \)
6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов \( R_1 \) и \( R_2 \) равны. Чему равно сопротивление каждого резистора?
1) 81 Ом
2) 18 Ом
3) 9 Ом
4) 4,5 Ом
7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?
1) 1/3 Ом
2) 3 Ом
3) 9 Ом
4) 27 Ом
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 10 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 5 Ом?
1) 9 Ом
2) 11 Ом
3) 16 Ом
4) 26 Ом
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 3 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 10 Ом?
1) 9 Ом
2) 10 Ом
3) 14 Ом
4) 24 Ом
10. Если ползунок реостата (см. схему) переместить влево, то сила тока
1) в резисторе \( R_1 \) уменьшится, а в резисторе \( R_2 \) увеличится
2) увеличится в обоих резисторах
3) в резисторе \( R_1 \) увеличится, а в резисторе \( R_2 \) уменьшится
4) уменьшится в обоих резисторах
11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?
Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) сопротивление реостата 2
Б) сила тока в цепи
B) напряжение на резисторе 1
ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется
12. Установите соответствие между физическими величинами и правильной электрической схемой для измерения этих величин при последовательном соединении двух резисторов \( R_1 \) и \( R_2 \). Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе \( R_1 \) и \( R_2 \)
Б) напряжение на резисторе \( R_2 \)
B) общее напряжение на резисторах \( R_1 \) и \( R_2 \)
Часть 2
13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов \( R_1 \) = 10 Ом, \( R_2 \) = 5 Ом, \( R_3 \) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?