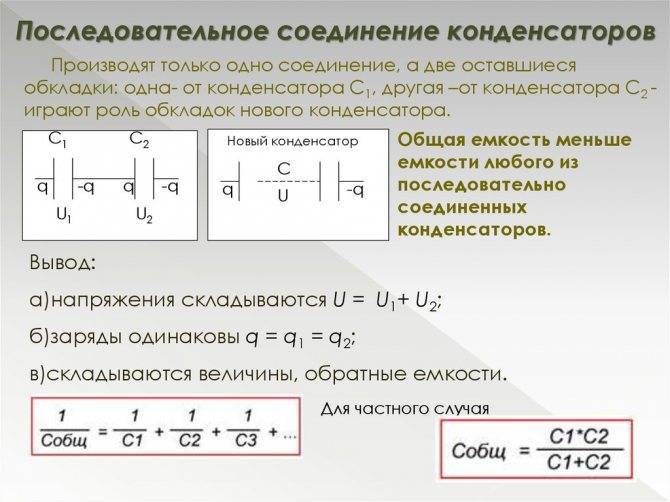
Формула индуктивного сопротивления

Содержание

Индуктивное сопротивление катушки

Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением. Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.

Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.

При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).

Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.

Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.

Индуктивное сопротивление обозначается буквой XL и измеряется в омах.

Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле

XL=2π• f •L

где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн

Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:

Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.

Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.

Источник

Взаимоиндуктивное сопротивление

Сопротивление в электрической цепи, обусловленное взаимоиндукцией, аналогично сопротивлению, обусловленному самоиндукцией, так как э. д. с. взаимоиндукции влияет на режим цепи с качественной стороны так же, как и э. д. с. самоиндукции.

Одноименные и разноименные зажимы индуктивно-связанных катушек
Ранее было дано определение согласного и встречного включения катушек.
При согласном включении магнитные потоки самоиндукции и взаимоиндукции в обеих катушках по направлению совпадают, поэтому э. д. с. самоиндукции и взаимоиндукции в каждой катушке также направлены одинаково.

При встречном включении магнитные потоки, а также э. д. с. самоиндукции и взаимоиндукции по направлению противоположны.

На схемах замещения взаимная индуктивность обозначается буквой М и дугой, объединяющей два индуктивно-связанных элемента (рис. 16.1). Для того чтобы различать согласное и встречное включения, на схемах обозначают также начала индуктивно-связанных катушек, отмечая их точками или звездочками.

Зажимы индуктивно-связанных катушек называют одноименными (начала или концы), если при согласном включении положительное направление токов, принятое на схеме, относительно этих зажимов одинаково (рис. 16.1, а). При встречном включении (рис. 16.1, б) ток в одной катушке направлен к началу, а в другой — к концу.

Разметка зажимов на основе опыта

Направление магнитных потоков катушек зависит от их взаимного расположения и направления намотки витков. При отсутствии сведений о расположении начал и концов можно провести простой опыт, для которого кроме самих индуктивно-связанных катушек требуется гальванический элемент (или аккумулятор) и гальванометр (рис. 16.2).

Рис. 16.2. Схема опыта для разметки зажимов катушек

Одну из катушек через ключ присоединяют к гальваническому элементу, к зажимам другой подключают гальванометр. В момент замыкания ключа К возникают токи в обеих катушках, причем ток i₂ создает магнитный поток, направленный навстречу потоку первой катушки (правило Ленца). Поэтому при включении гальванического элемента токи i₁ и i₂ направлены противоположно относительно одноименных зажимов. Направление тока i₁ известно, так как известна полярность источника питания, а направление тока i₂ определяется по отклонению гальванометра.

Ток i₂ направлен к положительному зажиму гальванометра, если стрелка его отклоняется по шкале (шкала односторонняя).

Одноименными зажимами катушек являются зажимы, к которым присоединены положительные зажимы источника и гальванометра; другие два зажима также одноименны.

Активное и реактивное сопротивление

Реактивная составляющая встречается в двух формах: емкостной (она присуща конденсаторным устройством) и индуктивной (свойственна трансформаторам, катушкам и обмоткам). Для определения отношения между напряжением и токовой силой требуется знать показатели всех видов оказываемого проводником сопротивления.

Реактивное сопротивление

Когда конденсатор подсоединен в электроцепь, за временной период до смены полярности он успевает набрать только некоторый процент заряда. Частота тока прямо пропорциональна величине заряда, набираемой элементом. Реактивный эффект на конденсаторном элементе наблюдается из-за того, что у него есть емкость. Когда частота возрастает, емкостное противодействие падает. Благодаря этому эффекту, данные детали хорошо подходят для использования в роли шунта с меняющейся величиной.

У катушки при увеличении токовой частоты растет и индуктивное противодействие. Помимо частоты, на значение также сильно влияет обмоточная индуктивность.

Важно! Бывает, что результирующая реактивная составляющая в цепи с несколькими обмотками и конденсаторами оказывается равной нулю. В таком случае фазы напряжения и электротока совпадают

Если между ними есть хоть какая-то разница фаз в ту или другую сторону, реактивная компонента будет отличной от нуля.

В реальности детали электрической цепи имеют как активную, так и обе реактивных составляющих. Но в ряде случаев одной или двумя из них принято пренебрегать из-за очень малых показателей, незначительно влияющих на общую ситуацию в сети. К примеру, обычно принимают, что конденсатор (если пренебречь энергетическими потерями) имеет исключительно емкостное противодействие

У лампочек накаливания, в свою очередь, принимается во внимание только активная компонента. У обмоточных элементов выделяются активная и индуктивная составляющие

Катушка индуктивности в цепи переменного тока

Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится осциллограф, генератор частоты, собственно сама катушка индуктивности и резистор на 100 Ом. Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.Он у меня будет в качестве шунта. Падение напряжения на этом резисторе будет зависеть от тока, протекающего через него

Собираем все это дело по такой схеме:

Получилось как то так:

Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал — желтым. Следовательно, красная синусоида — это частота, которую нам выдает генератор частоты, а желтая синусоида — это сигнал, который снимается с резистора.

Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе.

Опыт N1

Для начала подаем сигнал с частотой в 1 Килогерц.

Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф

Красный кружок с цифрой «1» — это замеры «красного»канала. Как мы видим, F (частота) =1 Килогерц, а Ма (амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой «2». F=1 Килогерц, а Ма=1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе.

Увеличиваем частоту до 10 Килогерц

Амплитуда не уменьшилась. Сигнал какой есть, такой и остался.

Увеличиваем до 100 Килогерц

Заметили разницу? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется сдвиг фаз. Красный сигнал никуда не сдвигается, запаздывает именно желтый. Это имейте ввиду.

Сдвиг фаз — это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:

Увеличиваем частоту до 200 Килогерц

На частоте 200 Килогерц амплитуда упала вдвое, да и разность фаз стала больше.

Увеличиваем частоту до 300 Килогерц.

Амплитуда желтого сигнала упала уже до 720 милливольт. Разность фаз стала еще больше.

Увеличиваем частоту до 500 Килогерц

Амплитуда уменьшилась до 480 милливольт.

Добавляем еще частоту до 1 Мегагерц

Амплитуда желтого канала стала 280 милливольт.

Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 Мегагерца

Амплитуда «желтого» сигнала стала настолько маленькой, что мне пришлось ее даже увеличить в 5 раз.

И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2.

Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок:

Так какой вывод можно сделать?

С увеличением частоты сопротивление катушки растет, а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов.

Опыт N2

Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микрогенри.

Итак, прогоняем все по тем же значениям частоты

При частоте в 1 Килогерц у нас значение почти не изменилось.

10 Килогерц

Здесь тоже ничего не изменилось.

100 Килогерц

Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонько сдвигаться.

200 Килогерц

Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты.

300 Килогерц

Сдвиг фаз стал больше и амплитуда просела еще больше

500 Килогерц

Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела.

1 Мегагерц

Амплитуда желтого сигнала падает, сдвиг фаз прибавляется.

2 Мегагерца, предел моего генератор частоты

Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта.

Обратите внимание на амплитуду в Вольтах на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом

Отсюда вывод напрашивается сам собой:

При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается.

Треугольник сопротивления

В цепи постоянного тока отношение напряжения к току называется сопротивлением. Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.

Если мы разделим стороны треугольника напряжения выше на ток, получим еще один треугольник, стороны которого представляют сопротивление, реактивное сопротивление и полное сопротивление катушки. Этот новый треугольник называется «Треугольник сопротивления».

Расчет параметров катушки

Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.

Расчет L в зависимости от заданной конструкции

Если исходными параметрами являются: w, D каркаса и длина намотанного провода, то формула для расчёта имеет вид:

L = 0,01*D*w2/(l/D) + 0,46,

где:

D – диаметр каркаса, см;
w – число витков;
l – длина намотки, см;
L – индуктивность, мкГн.

Подставляя численные значения в формулу, получают значение L.

Расчет количества витков по индуктивности

Зная D каркаса и L, рассчитывают количество витков в катушке, формула имеет вид:

w = 32*√(L*D),

где:

L – индуктивность, мкГн;
D – диаметр каркаса, мм.

Если в качестве исходных параметров берутся длина навитого в ряд проводника и его диаметр, то количество витков находят, используя формулу:

w = l/d,

где:

l – длина намотки, мм;
d – диаметр провода, мм.

Измерения диаметра провода проводят линейкой или штангенциркулем.

Расчёт индуктивности прямого провода

Собираясь найти L круглого прямого проводника, обращаются к приближённой формуле:

L = (μ0/2π)*l*( μe*ln(l/r) + 1/4* μi,

где:

μ0 – магнитная постоянная;
μe – относительная магнитная проницаемость (ОМП) среды (для вакуума – 1);
μi – ОМП проводника;
l – длина провода;
r – радиус провода.

Формула справедлива для длинного проводника.

Расчёт однослойной намотки

Однослойные дроссели без сердечника легко и быстро можно рассчитать при помощи онлайн-калькулятора, в окно которого можно забить все известные характеристики, и программа выдаст значение L.

Вычисления проводятся и вручную, с использованием математического выражения. Оно имеет вид:

L = D2*n2/45D + 100*l,

где:

D – диаметр катушки, см;
l – длина намотанного провода, см;
n – количество витков.

Формула подходит для вычислений L дросселей без ферритовых сердечников.

Однослойная катушка виток к витку

Дроссель с сердечником

При наличии сердечника следует учесть его размеры и форму. В случае одинаковых катушках индуктивность больше у той, которая располагается на сердечнике.

Расчёт однослойной намотки с сердечником

Многослойная намотка

Особенности расчёта при подобном способе наматывания провода заключаются в том, что нужно учитывать его толщину. Формула для дросселя без сердечника имеет вид:

N²=(L*(3Dk+9l+10t))/0.008Dk²,

где:

Dk – общий диаметр (диаметр каркаса и намотки);
t – толщина слоя;
l – длина накрученного провода.

Все значения подставляют в мм, величину L – в мкГн.

Многослойная намотка

Конструкция

Главное назначение катушек индуктивности ГОСТ 20718-75 – это накопление электрической энергии в пределах магнитного поля для акустики, трансформаторов и т. д. Их используют для разработки и конструирования различных селективных схем и электрических устройств. От конструкции (материала, количества витков), наличия каркаса зависит их функциональность, размеры и область использования. Изготовление устройств производится на заводах, но можно сделать их самостоятельно. Самодельные элементы несколько уступают по надежности профессиональным, но обходятся в разы дешевле.

Фото — схема

Каркас катушки индуктивности выполняется из диэлектрического материала. На него наматывается изолированный проводник, который может быть как одножильным, так и многожильным. В зависимости от типа намотки, они бывают:

Спиральными (на ферритовом кольце);
Винтовыми;
Винтоспиральными или комбинированными.

Примечательной особенностью катушки индуктивности для электрических схем является то, что её можно намотать как в несколько слоев, так и нированно, т. е., с обрывками Если используется толстый проводник, то элемент может обматываться без каркаса, если тонкий – то только на рамку. Эти каркасы катушек индуктивности бывают различного сечения: квадратные, круглые, прямоугольные. Полученная намотка может вставляться в специальный корпус какого-либо электрического устройства или использоваться в открытом виде.

Фото — конструкция самодельного элемента

Для увеличения индуктивности используются сердечники. В зависимости от назначения элемента, варьируется используемый материал стержня:

С ферромагнитным и воздушным сердечником применяются при высоких частотах тока;
Стальные используются в условиях низкого напряжения.

Вместе с этим, в электротехнике активно используются индуктивные классические катушки без сердечника, которые можно сделать своими руками при помощи намотки на немагнитный контур.Такие устройства имеют некоторые преимущества перед «сердечными». У них большая линейность импеданса. Но, у тороидальной модели намотка на немагнитный каркас способствует появлению паразитной емкости.

Исходя из принципа работы, бывают такие типы:

Контурные. Преимущественно используются в радиотехнике для создания колебательных контуров платы, работают вместе с конденсаторами. Для соединения используется последовательное подключение. Это современный вариант плоской контурной катушки Тесла;
Вариометры. Это высокочастотные перестраиваемые катушки, индуктивностью которыми можно при необходимости управлять при помощи дополнительных устройств. Они представляют собой соединение двух отдельных катушек, при этом, одна подвижна, а вторая нет;
Сдвоенные и подстроечные дроссели. Основные характеристики этих катушек: малое сопротивление постоянному току и высокое переменному. Дроссели изготавливаются из нескольких катушек, соединенных обмотками между собой. Их часто используют в виде фильтра для различных радиотехнических приборов, устанавливают для контроля помех в антенны и т. д.;
Трансформаторы связи. Их конструктивной особенностью является то, что на одном стержне установлено от двух и более катушек. Они используются в трансформаторах для обеспечения определенной связи между отдельными компонентами устройства.

Маркировка катушек индуктивности определяется по количеству витков и цвету корпуса.

Фото — маркировка

Принцип действия индуктивного сопротивления линий

Именно индуктивность признана главной характеристикой для катушек наряду с аналогичным показателем для их обмоток. R реактивного вида, проявляющееся под действием самоиндукционной ЭДС, растет в прямой пропорции с частотой тока.

Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.

Оперативно справиться с поставленной задачей по расчету номинальных показателей помогут специальные таблицы. В них для самых распространенных проводников приведены все главные характеристики. Но на практике часто требуется узнать Х для участка с конкретной протяженностью. В этом случае главным инструментом является уже приводившееся выражение

Ёмкостное сопротивление

Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.

Мы можем использовать следующие соотношения:

Попробуй обратиться за помощью к преподавателям

Если $I(t)$ определена уравнением (1), то заряд выражен как:

где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:

Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac<pi ><2>.$ Амплитуда напряжения на емкости равна:

Величину $X_C=frac<1><omega C>$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.

Активное сопротивление

И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента — резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, «активный — это деятельный, энергичный, проявляющий инициативу». Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.

От чего зависит?

Зависит показатель от температуры и отличается в разных материалах.

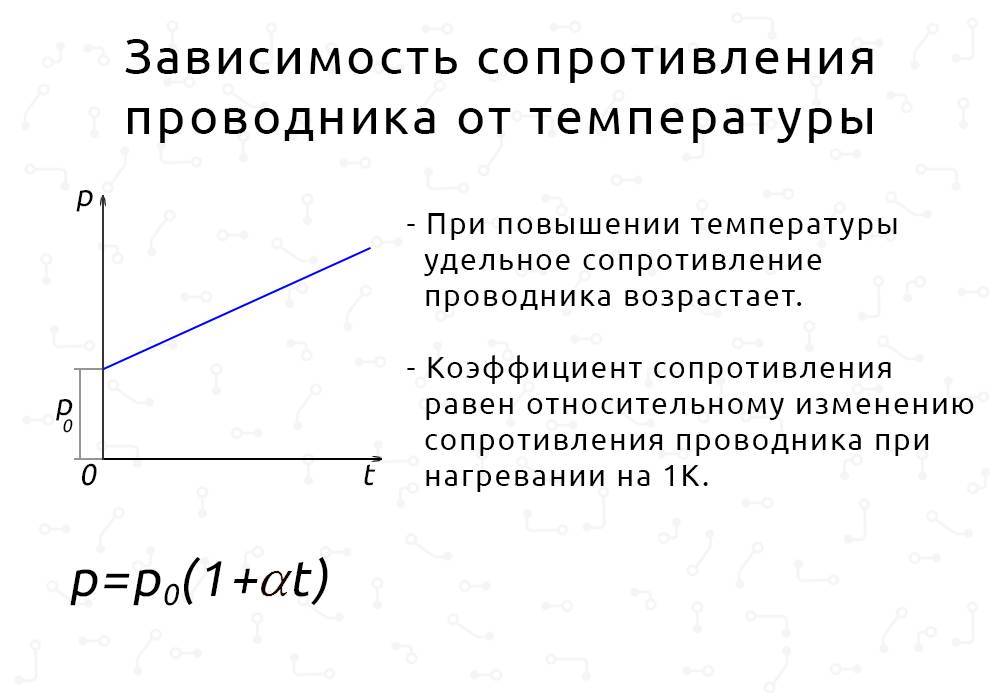
Зависимость от температуры

В каждом наименовании материала он отличается, в частности:

В проводниковых элементах при увеличении показателя температуры, возрастает.
В то же время в полупроводниковых, а также диэлектриках на таких же условиях уменьшается.

Величину, которая учитывает параметр изменения, принято называть температурным коэффициентом.

Удельное сопротивление разных материалов

Рассмотрим показатель монокристаллов, при параметре температуры, равном 20 градусов.

Олово	9,9–14,3
Висмут	109–138
Кадмий	6,8–8,3
Цинк	5,91–6,13
Теллур	2,90х109–5,9х109

Таблица для металлов

В таблице приводятся показатели для металлов, а также отдельных сплавов. Разница параметров связана непосредственно с химической чистотой, методами отливки, непостоянством самого сплава.

Серебро	0,015–0,0162
Медь	0,01707–0,018
Золото	0,023
Алюминий	0,0262–0,0295
Иридий	0,0474
Натрий	0,0485
Молибден	0,054
Вольфрам	0,053–0,055
Цинк	0,059
Индий	0,0837
Никель	0,087
Железо	0,099
Платина	0,107
Олово	0,12
Свинец	0,217–0,227
Титан	0,5562–0,7837
Ртуть	0,958
Висмут	1,2

Что надо знать про электрические процессы

Если говорить простым языком, то под сопротивлением принято понимать свойство среды, по которой протекает электрический ток, снижающее его величину.

Так работают провода и изоляторы высоковольтной линии электропередач, показанные на верхней картинке, да и любое вещество.

Изоляторы обладают очень высокими диэлектрическими свойствами, изолируют высоковольтное напряжение, присутствующее на токоведущих шинах от контура земли. Это их основное назначение.

Провода же должны максимально эффективно передавать транслируемые по ним мощности. Их создают так, чтобы они обладали минимальным электрическим сопротивлением, работали с наименьшими потерями энергии на нагрев.

В этом случае передача электричества от источника напряжения к потребителю на любое расстояние будет проходить эффективно.

Приведу для примера картинку из предыдущей моей статьи.

Ее, как и верхнюю, можно представить таким обобщенным видом.

На внешнем участке цепи токоведущие жилы отделены друг от друга воздушной средой и слоем изоляции с высокими диэлектрическими свойствами.

Хорошей проводимостью обладают токоведущие жилы. Подключенный к ним электрический прибор функционирует оптимально.

Как работает резистор

Ток в металлах проходит под действием приложенного напряжения за счет направленного движения электронов. При этом они соударяются, встречаются с положительно и отрицательно заряженными ионами.

Такие столкновения повышают температуру среды, уменьшают силу тока.

За направление электрического тока в электротехнике принято движение заряженных частиц от плюса к минусу. Электроны же движутся от катода к аноду.

Электрическое сопротивление металла зависит от его структуры и геометрических размеров.

Аналогичные процессы протекают в любой другой токопроводящей среде, включая газы или жидкости.

Какие существуют виды сопротивлений

В домашних электрических приборах используется большое разнообразие резисторов с постоянной или регулируемой величиной.

Они ограничивают величину тока всех бытовых устройств, а в наиболее сложных модулях их количество может достигать тысячи или более. Резисторы работают практически во всех схемах.

При использовании в цепях переменного тока они обладают активным сопротивлением, а конденсаторы и дроссели — реактивным.

Причем, на конденсаторах создается емкостное сопротивление, а у дросселей — индуктивное.

Реактивная составляющая на конденсаторах и дросселях сильно зависит от частоты электромагнитного колебания.

2 Шутки электриков о токах через конденсатор и дроссель

Их я привожу потому, что они позволяют запомнить характер прохождения тока через реактивные элементы.

Шутка №1 о емкости

В домашней сети и внутри многих приборов работают переменный и постоянный токи. Они по-разному ведут себя, если встречают на своем пути конденсатор.

Поскольку он состоит из двух токопроводящих пластин, разделенных слоем диэлектрика, то его обозначают на схемах двумя жирными черточками, расположенными параллельно. К их серединам подключены провода, нарисованные перпендикулярными линиями.

Переменный ток имеет форму гармоничной синусоиды, состоящей из двух симметричных половинок.

Такая гармоника движется от начала координат, встречает на своем пути обкладки, переваливается через них и, скатившись, начинает обгонять приложенное напряжение.

Постоянный ток таким свойством не обладает. Его тупой конец просто упирается в обкладку и останавливается. Пройти через конденсатор он не может. Это для него непреодолимое препятствие.

Шутка №2 о дросселе

Индуктивность выполнена витками изолированного провода. Любой ток проходит по нему. Но синусоида своими волнами путается в витках катушки, начинает отставать от напряжения.

Постоянка же спокойно перемещается внутри провода дросселя без ощущения какого-либо значительного противодействия. Поэтому постоянное напряжение может своим током спалить дроссель, созданный для работы на переменке.

Что же это за зверь: сверхпроводимость

Сто лет назад выявлена способность определенных металлов полностью терять свое сопротивление электрическому току при сверхнизких температурах. Выглядит этот процесс следующим образом.

Со сверхпроводниками домашний мастер не работает

Но на верхнюю часть приведенного графика рекомендую обратить внимание: нагрев металла повышает его электрическое сопротивление

При электротехнических расчетах, требующих получения точного результата, необходимо учитывать температурный коэффициент, взятый из справочников.

Закон Ома для цепей переменного тока

называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.

Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $
u$.

Решение:

Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.

Амплитудное значение силы тока выражается «законом Ома для переменного тока»:

оно связано с действующим значением силы тока как:

В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу:

Подставим в формулу (1.2) формулы (1.1) и (1.3), получим:

где $omega =2pi
u .$

Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$).

Решение:

Используем результат примера 1. Напряжение на катушке индуктивности выражается формулой:

Напряжение на активном сопротивлении ($U_R$) равно:

Напряжение на конденсаторе ($U_C$) определяется как:

Так и не нашли ответ на свой вопрос?

Просто напиши с чем тебе нужна помощь

В данной статье мы подробно поговорим про индуктивное сопротивление, реактивное сопротивление и треугольники напряжения, сопротивления и силы.